今回はシンプルな質量-ばねシステム(Mass Spring System)を用いて、このモデルの振動について算出していきたいと思います。
質量-ばねシステムの運動方程式
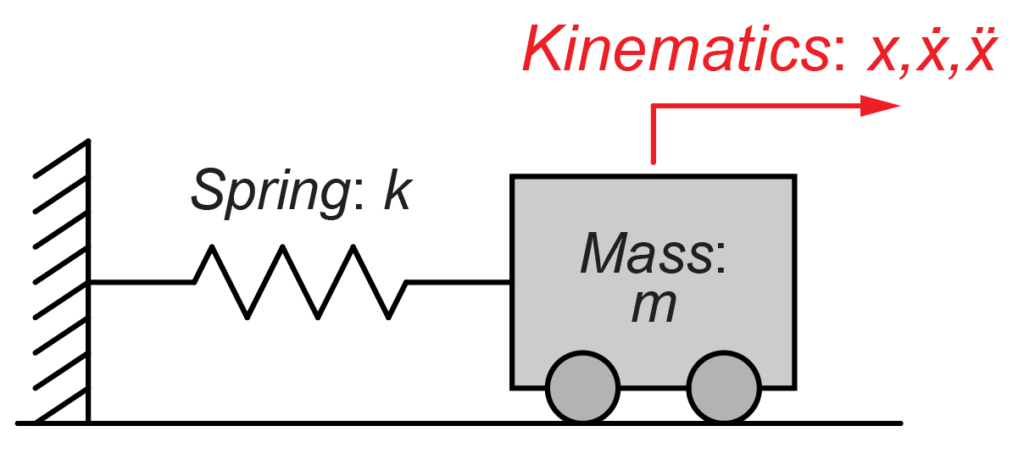
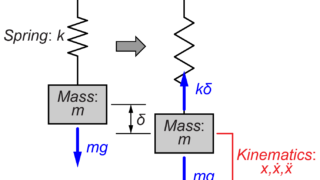
今回扱うシステムは、図のように質量\(m\)がばね\(k\)で壁に繋がれたモデルです。
初期条件として、時刻\(t=0\)で変位\(x(t)\)が\(x(0)=x_0\)、速度\(\dot{x}(t)\)が\(\dot{x}(0)=0\)とします。
質量\(m\)の変位\(x(t)\)について、ばね\(k\)が伸びる向きを正(プラス)とすると、このシステムの運動方程式は、
$$ ma=F$$
$$ \Rightarrow m \ddot{x}(t) = – k x(t) $$
となります。
この微分方程式(運動方程式)を\(x(t)\)について解くことで、質量\(m\)の振動を求めることが出来ます。
質量-ばねシステムの振動
先ほど求めた微分方程式を解いていきます。
$$ m \ddot{x}(t) + k x(t) = 0 $$
求める二階微分方程式の一般解\(x(t)\)を
$$ x(t) = C_1 cos (\omega_1 t) + C_2 sin (\omega_2 t) $$
とすると、
$$ \dot{x}(t) = – C_1 \omega_1 sin (\omega_1 t) + C_2 \omega_2 cos (\omega_2 t) $$
$$ \ddot{x}(t) = – C_1 {\omega_1}^2 cos (\omega_1 t) – C_2 {\omega_2}^2sin (\omega_2 t) $$
となります。
これらと初期条件、
$$ x(0)=x_0 $$
$$ \dot{x}(0)=0 $$
を組み合わせて、\(x(t)\)について解いて聞きます。
時刻\(t=0\)で変位\(x\)が\(x_0\)なので、
$$ x(0) = C_1 cos (\omega_1 \cdot 0) + C_2 sin (\omega_2 \cdot 0) = x_0 $$
$$ \Rightarrow C_1 = x_0 $$
となります。
同様に時刻\(t=0\)で速度\(\dot{x}\)が0なので、
$$ \dot{x}(0) = – C_1 \omega_1 sin (\omega_1 \cdot 0) + C_2 \omega_2 cos (\omega_2 \cdot 0) = 0 $$
$$ \Rightarrow C_2 = 0 $$
となります。
そして、これら\(C_1\)と\(C_2\)を微分方程式に代入すると、
$$ \ddot{x}(t) + \frac{k}{m} x(t) = 0 $$
$$ \Rightarrow – x_0 {\omega_1}^2 cos (\omega_1 t) + \frac{k}{m} x_0 cos (\omega_1 t) = 0 $$
$$ \Rightarrow \omega_1 = \sqrt{ \frac{k}{m} } $$
となります。
よって、今回の質量-ばねシステムの振動は、
$$ x(t) = x_0 cos \left(\sqrt{ \frac{k}{m} } t \right) $$
と表すことが出来ます。
まとめ
今回は質量-ばね系モデルを用いて、システムの振動を実際に求めてみました。
次回は、すこし複雑なモデルの振動を算出していきたいと思います。

























 ELEGOO Arduinoスターターキット
ELEGOO Arduinoスターターキット

 UNO R3スマートロボットカー
UNO R3スマートロボットカー

 Raspberry Pi 3 Model b+
Raspberry Pi 3 Model b+
