制御工学の基本　PID制御をマスターしてロボットを動かそう

PID制御とはフィードバックを用いた古典制御の中の一つです。

その名の通り、現在の出力値\(ｙ\)について目標値\(ｒ\)との偏差\(e\)（Propotional）とその値の積分（Integral）や微分（Differential）の3要素を用いて制御を行います。

今回は制御対象のシステムとして、

$$ G_p = \exp(-0.2 s) \frac{1}{9 s^2 + 9 s + 2} $$

の二次遅れ系を使用しました。

この制御システムの意味が分からなくても、PID制御は理解できるように説明しますので、安心してください。

P制御

P制御（比例制御）は、出力値と目標値の偏差\(e\)に対して、比例ゲイン\(K_p\)を用いてフィードバック制御を行う方法です。

時刻\(ｔ\)で出力値\(ｙ\)と目標値\(ｒ\)の時、その偏差\(e\)は、
$$ e (t) = r (t) – y (t) $$
となります。

P制御の入力\(u\)は、この偏差\(e\)に対して比例ゲイン\(K_p\)を掛け合わせたものとなります。

$$ u (t) = K_p e (t) $$

この入力を制御対象に送り目標値に対する制御を行います。

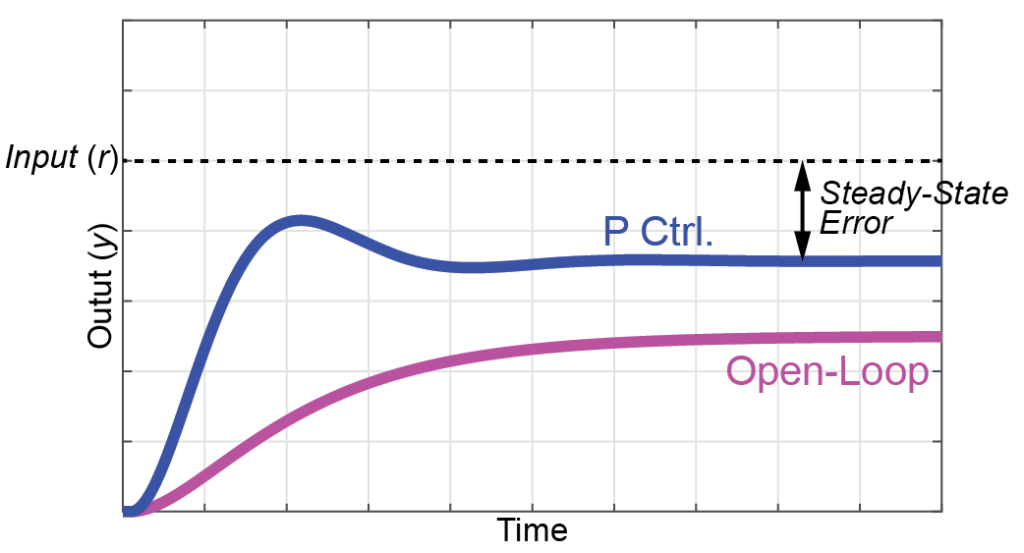
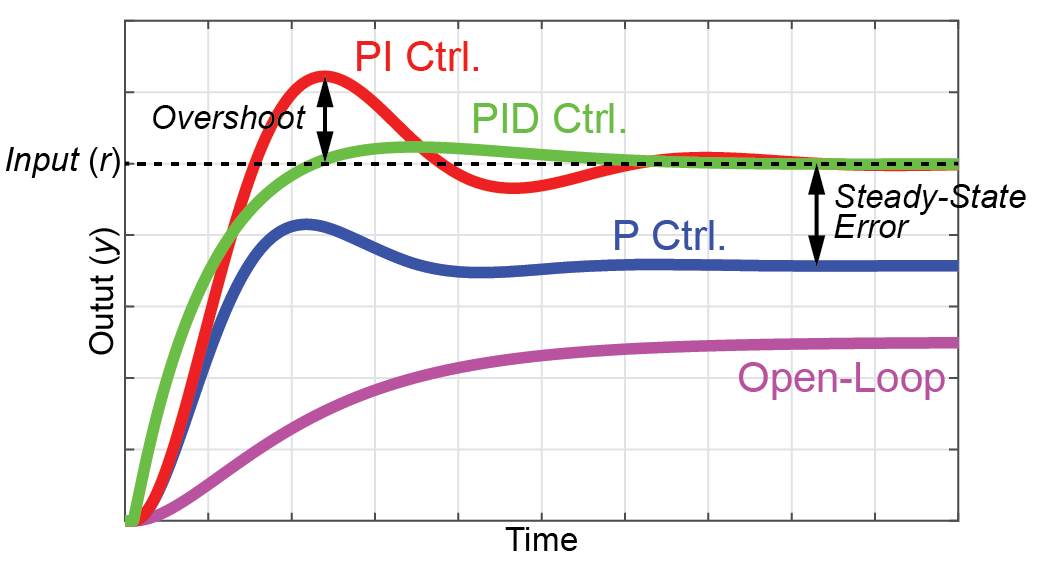
この比例ゲインKpが高ければ高いほど目標値に到達する時間が短くなります。

しかしP制御には問題があります。

時間が進むと目標値に対して出力値との偏差eがどんどん小さくなります。

そのため、目標値に達するための十分な入力値にならず、定常偏差（オフセット）と呼ばれる誤差が発生します。

PI制御

P制御での問題を解消するために、PI制御を行います。

PI制御では、P制御で追加した比例ゲイン\(K_p\)に加えて積分ゲイン\(K_i\)を用います。
この\(K_i\)を偏差\(e\)の時間積分に掛け合わせることでI制御を行います。

$$ u (t) = K_p e (t) + K_i  \displaystyle \int_{0}^{t} e (\tau) d\tau $$

偏差\(e\)の時間積分に対する制御をすることで、偏差\(e\)が長く存在した場合（P制御で問題となった定常偏差が発生しているような場合）に、その分だけ入力\(u\)を大きくして、目標に近づけることが出来ます。

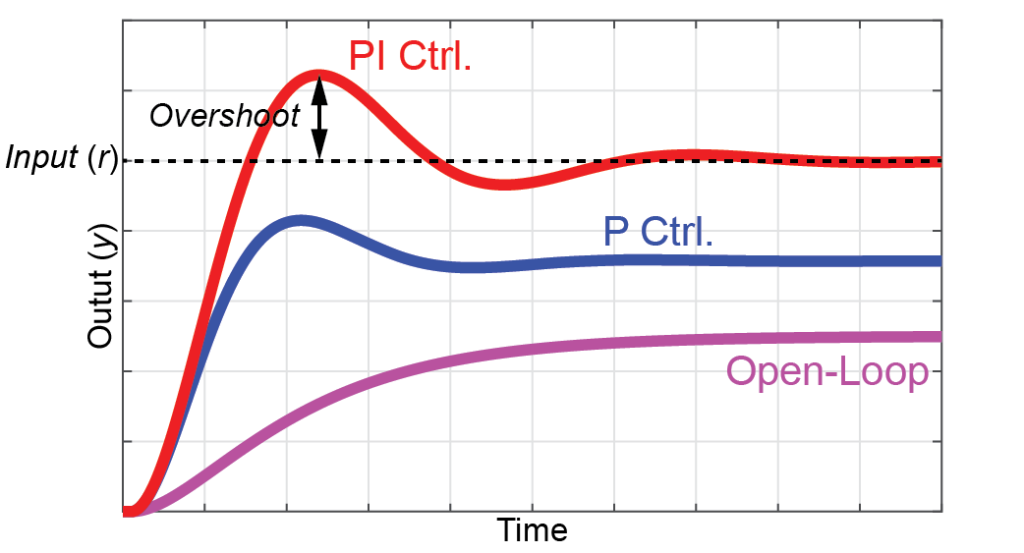
このPI制御はP制御の問題点を解決してくれますが、新たな問題もあります。

PI制御の問題は、目標値を行き過ぎる（オーバーシュート）ことや、目標値周辺を振動する現象が発生することです。

PID制御

PI制御の問題を解決するために、微分ゲイン\(K_d\)を追加します。これをPID制御と言います。

$$ u (t) = K_p e (t) + K_i  \displaystyle \int_{0}^{t} e (\tau) d\tau + K_d  \frac{d e(t)}{dt} $$

この微分ゲイン\(K_d\)は偏差\(e\)の時間微分に掛け合わせることで、PI制御の効果に加えて、急激な出力値の変化を抑えることが出来ます。

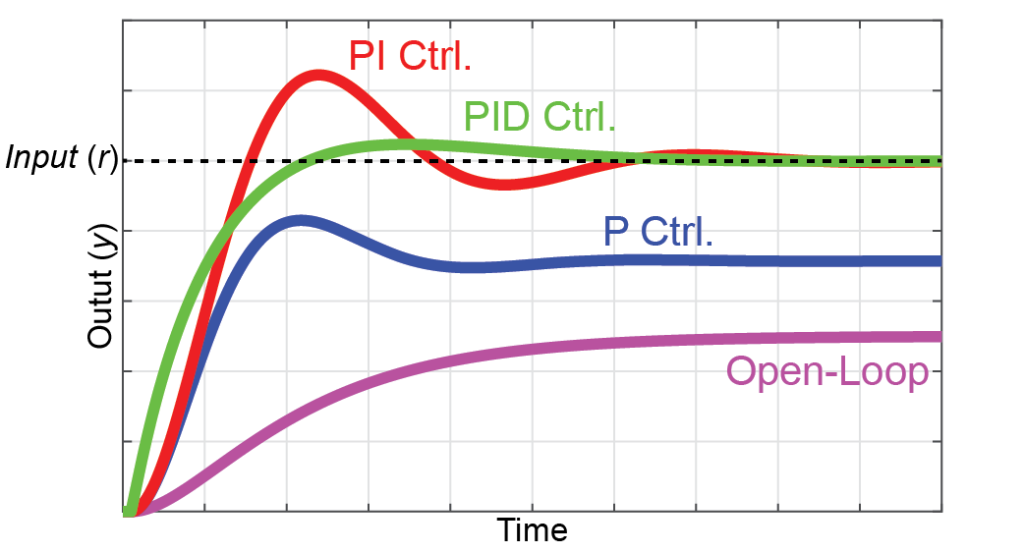
まとめ

PID制御では適切に各ゲインの値（\( K_p, K_i, K_d \)）を決定することで、制御対象\(G_p\)を自由に制御することが可能になります。

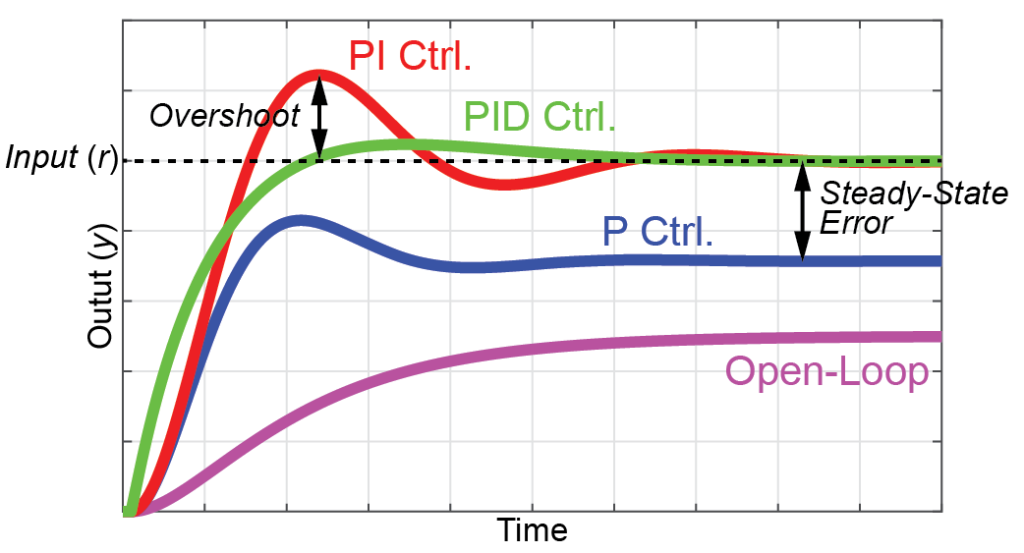
この適切なゲインを決定する方法は色々と提案されていますが、未だにシミュレーションを用いて試行錯誤的に決定する場合が多くあります。