回転体によるシステムの振動を運動方程式で表す（Rotating Unbalance）

質量内を回転する物体によって生じる振動をシステムの運動方程式を用いて表したいと思います。

このようなシステムをRotating Unbalanceと言います。

（すみません。日本語で何と言えば良いか分かりません。）

Rotating Unbalanceモデル

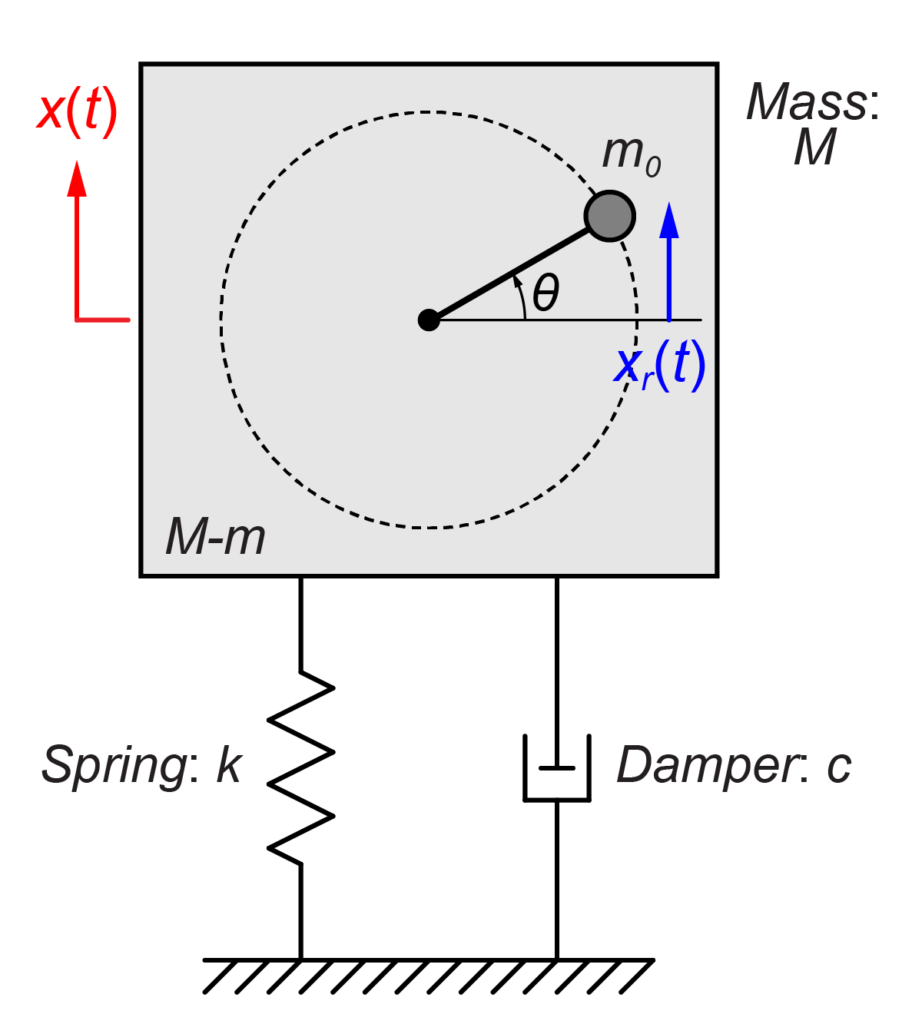
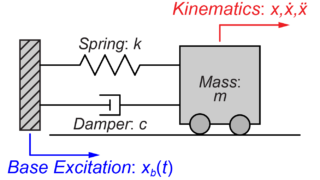
今回は、図のような全体の質量\(M\)のシステムが、ばね\(k\)とダンパー\(c\)で地面に接続されている質量-ばね-ダンパーモデルを扱います。

質量\(m\)の物体が内部で

$$ x_r(t) = e \sin (\omega t) $$

と回転することによって、システム全体が振動します。

この時の振動をシステムの運動方程式を用いて算出したいと思います。

今回は、問題を簡略化するため縦方向の動き\(x(t)\)のみを考慮します。

つまりシステムが上下方向にしか動かないという前提で計算を進めていきます。

ラグランジュ方程式を用いた運動方程式の算出

今回は、システムの運動方程式を求めるために、システムのエネルギーを計算し、ラグランジュ方程式を用いることで運動方程式を算出したいと思います。

システムの各エネルギーを

運動エネルギー（Kinetic Energy: \(KE\)）

位置エネルギー（Potantial Energy: \(PE\)）

損失エネルギー（Energy Loss: \(R_{NC}\)）

と定義すると、ラグランジュ方程式から、

$$ \frac{d}{dt} \left( \frac{\partial}{\partial \dot{x}} KE \right) + \frac{\partial}{\partial \dot{x}} R_{NC} + \frac{\partial}{\partial x} PE = 0$$

と表すことが出来ます。

この式から、システムの運動方程式を求めることが出来ます。

システムの各エネルギーを算出

運動エネルギー：\(KE\)

このシステムの運動エネルギーは、回転する質量\(m\)の物体の運動エネルギーとその周りの物体（質量\(M-m\)）の運動エネルギーの合計になります。

よって、システムの運動エネルギーは、

$$ KE = \frac{1}{2}(M-m) \dot{x}(t)^2 + \frac{1}{2} m (\dot{x}(t)+\dot{x}_r(t))^2$$

と表すことが出来ます。

位置エネルギー：\(PE\)

このシステムの位置エネルギーは、ばね\(k\)とその変位\(x(t)\)で求めることが出来ます。

よって、システムの位置エネルギーは、

$$ PE = \frac{1}{2} k x(t)^2 $$

と表すことが出来ます。

損失エネルギー：\(R_{NC}\)

このシステムの損失エネルギーは、ダンパー\(c\)とその速度\(\dot{x}(t)\)で求めることが出来ます。

よって、システムの損失エネルギーは、

$$ R_{NC} = \frac{1}{2} c \dot{x}(t)^2 $$

と表すことが出来ます。

システムの運動方程式

求めた各エネルギーをラグランジュ方程式に代入して運動方程式を求めます。

ラグランジュ方程式を用いた関係式から

$$ \frac{d}{dt} \left( \frac{\partial}{\partial \dot{x}} KE \right) + \frac{\partial}{\partial \dot{x}} R_{NC} + \frac{\partial}{\partial x} PE = 0$$

$$ \Rightarrow \frac{d}{dt} \left( \frac{\partial}{\partial \dot{x}} \left(\frac{1}{2}(M-m) \dot{x}(t)^2 + \frac{1}{2} m (\dot{x}(t)+\dot{x}_r(t))^2\right) \right) $$

$$+ \frac{\partial}{\partial \dot{x}} \left(\frac{1}{2} c \dot{x}(t)^2\right) + \frac{\partial}{\partial x} \left(\frac{1}{2} k x(t)^2\right) = 0$$

$$ \Rightarrow M \ddot{x}(t) + c \dot{x}(t) + k x(t) = – m \ddot{x}_r(t) $$

となるため、

$$ x_r(t) = e \sin (\omega t) $$

$$ \Rightarrow \ddot{x}_r(t) = – e \omega^2 \sin (\omega t) $$

から、システムの運動方程式は、

$$ \Rightarrow M \ddot{x}(t) + c \dot{x}(t) + k x(t) = m e \omega^2 \sin (\omega t) $$

と表すことが出来ます。

まとめ

今回はRotating Unbalanceモデルを用いて、物体がシステム内部で回転した際に生じる振動を求めるために、システムの運動方程式の求め方を紹介しました。