自動運転車を制御してみよう：簡単な制御モデルを求める

本シリーズは、実際に車やロボットの自動運転を行うために、必要な制御工学の情報を紹介しています。

自動運転車を制御してみよう 本シリーズでは、実際に車やロボットの自動運転を行うために必要な制御工学の情報を紹介していきます。 今回は、本シリー...

 

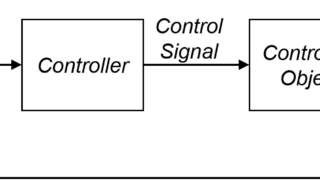
前回までの記事では、車の運動力学モデルを算出しました。

自動運転車を制御してみよう：車の運動力学モデルを求める 本シリーズでは、車やロボットの自動運転を実際に行うために必要となる制御工学の情報を紹介していきます。 https://ta...

 

今回は、自動運転モデルの問題を少し簡単化して、実際に車を自動制御する方法を紹介します。

 

簡単化した自動運転モデル

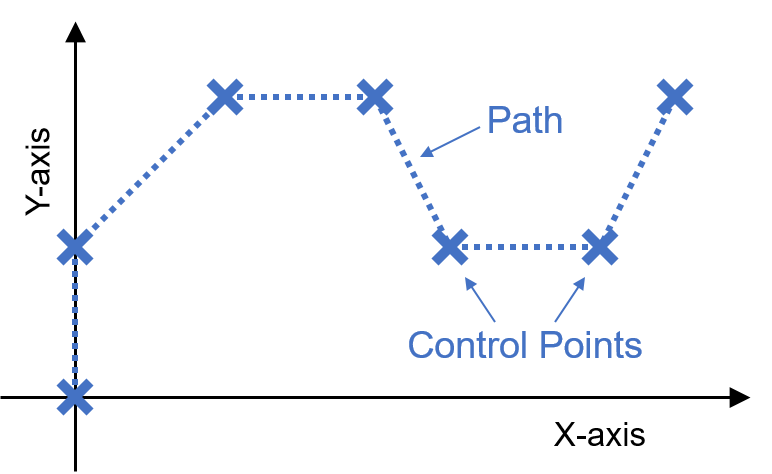
本シリーズでは、上の図のようにX-Y平面上で車の目標軌跡（Control Points and Path）が与えられた場合について、車を目標に沿って制御する方法を問題として扱っています。

 

今回は、このX-Y平面で与えられた軌跡を、下の図のようにX軸上のみに直線の目標軌跡が存在する問題に簡単化します。

 

 

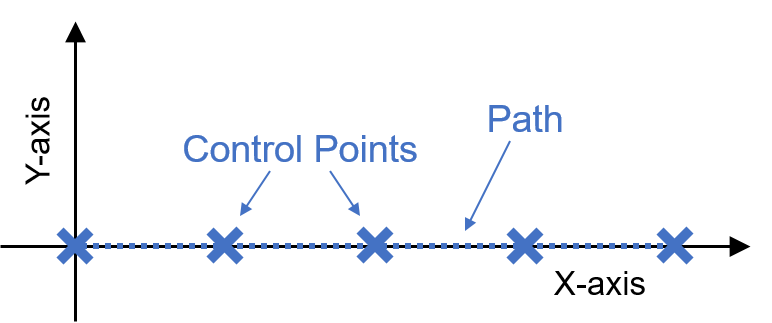
この簡単化した自動運転車の問題について、実際に車を目標軌跡に沿って制御する方法を考えていきます。

 

このように問題を簡単化することで、後で紹介する目標軌跡と車の位置の誤差を算出する計算や、車を制御するためのハンドル角度の算出がシンプルになります。

 

また、この目標軌跡がX軸上のみに存在するシンプルな問題を理解することで、先に紹介した目標がX-Y平面上に存在する場合の誤差やハンドル角度の計算の理解が容易になります。

 

車の位置と目標軌跡との誤差

時刻\(t\)での車の位置（\(x\)、\(y\)）と目標軌跡（X軸）との誤差を算出していきます。

 

目標軌跡がX軸上に存在するため、車と目標軌跡との誤差\(\varepsilon_p\)は常にY軸方向の誤差と同じになります。

 

ここで、目標軌跡がX軸上に存在するため目標のY軸成分の値は常に0になります。

 

よって、車の位置と目標軌跡との誤差\(\varepsilon_p\)は

$$ \varepsilon_p = y $$

のように、車の位置のY軸成分で求めることが出来ます。

 

また、目標軌跡に対する車の誤差角度\(\varepsilon_{\theta}\)は

$$ \begin{eqnarray} \varepsilon_{\theta} = \begin{cases} 90^{\circ} & ( y \gt 0 ) \\ 0^{\circ} & ( y = 0 ) \\ -90^{\circ} & ( y \lt 0 ) \end{cases}\end{eqnarray} $$

のように、求めることが出来ます。

 

これは、車のY軸成分（\(y\)）がプラス（\(+\)）の場合は、車の位置はX-Y平面上でX軸よりも上に存在することから、車の誤差角度\(\varepsilon_{\theta}\)は目標軌跡に対して\(90^{\circ}\)となるためです。

 

反対に、車のY軸成分（\(y\)）がマイナス（\(-\)）の場合は、車の位置はX-Y平面上でX軸よりも下に存在することから、車の誤差角度\(\varepsilon_{\theta}\)は目標軌跡に対して\(-90^{\circ}\)となる事も分かります。

 

例として、時刻\(t\)での車の位置が

$$ P = [x,y] = [2,1] $$

と与えられた場合、この車とX軸上の目標軌跡との誤差\(\varepsilon_p\)は

$$ \varepsilon_p = y = 1 $$

となり、この時の目標軌跡に対する車の誤差角度\(\varepsilon_{\theta}\)は

$$ \begin{eqnarray} y = 1 \gt 0 \\ \Rightarrow \varepsilon_{\theta} = 90^{\circ} \end{eqnarray} $$

となります。

 

ハンドルの角度を算出

次に、算出した誤差から車のハンドルの角度を算出していきます。

 

 

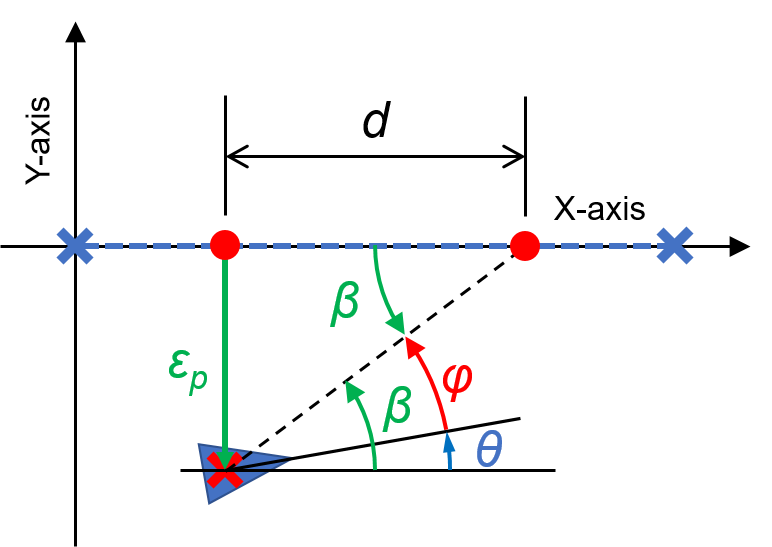
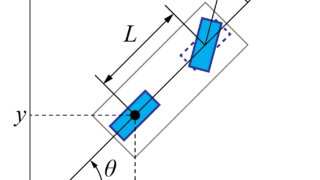
上の図のように表される車の位置と目標軌跡を考えます。

 

時刻\(t\)での車の位置とX軸上に存在する目標軌跡との誤差\(\varepsilon_p\)を用いると、車が目標軌跡に近づくために向くべき進行方向\(\beta\)は

$$ \beta = \arctan \left( \frac{\varepsilon_p}{d} \right)  $$

と表すことが出来ます。

 

ここで、距離\(d\)は車の現在位置から目標軌跡に到達する地点までの目標軌跡上での距離を示しています。

 

この車の向くべき進行方向\(\beta\)を表す式から、向くべき進行方向は車の位置と目標軌跡との誤差\(\varepsilon_p\)によって決定できることが分かります。

 

ここで、現在時刻での車の進行方向を\(\theta\)とすると、ハンドルの角度\(\phi\)は向くべき進行方向\(\beta\)より

$$ \phi = \beta – \theta $$

と算出することが出来ます。

 

これより、誤差\(\varepsilon_p\)が大きいほどハンドルを大きく切り、誤差\(\varepsilon_p\)が小さい場合はハンドルの角度を少しだけ変化させることが分かります。

 

また、車がY軸のマイナス側に存在する場合はハンドルを左に切り、Y軸のプラス側に存在する場合はハンドルを右に切ることで、目標軌跡に車の位置を近づけます。

 

シミュレーション結果比例定数を用いた自動運転制御

これまでに求めた車と目標軌跡との誤差\(\varepsilon_p\)からハンドルの角度\(\phi\)を算出する方法を用いて、実際に車を制御してみます。

 

条件１

まず１つ目のシミュレーション条件として、車の初期位置（\(x\)、\(y\)）と進行方向（\(\theta\)）を

$$ [x,y,\theta] = [0m,1m,0^{\circ}] $$

とし、X軸上の目標軌跡を追従する様子を取り扱います。

 

この時のハンドルの角度\(\phi\)を算出するために用いる距離\(d\)は

$$ d = 3 $$

を用います。

 

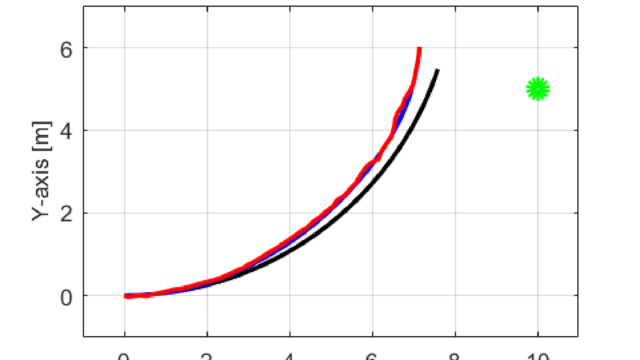
この条件の下でシミュレーションした結果は下図のようになります。

 

 

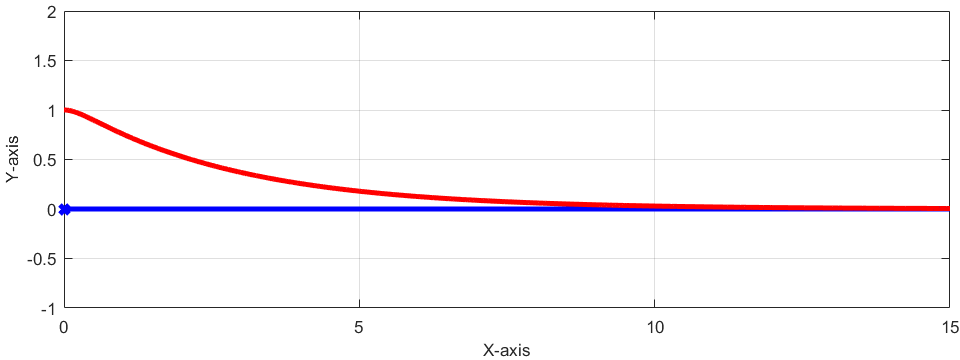
車の位置（赤線）が徐々に目標軌跡（青線）に近づいていることが分かります。

 

条件2

次に2つ目のシミュレーション条件として、車の初期位置（\(x\)、\(y\)）と進行方向（\(\theta\)）を

$$ [x,y,\theta] = [0m,-2m,0^{\circ}] $$

とし、X軸上の目標軌跡を追従する様子を取り扱います。

 

この時のハンドルの角度\(\phi\)を算出するために用いる距離\(d\)は

$$ d = 2 $$

を用います。

 

この条件の下でシミュレーションした結果は下図のようになります。

 

 

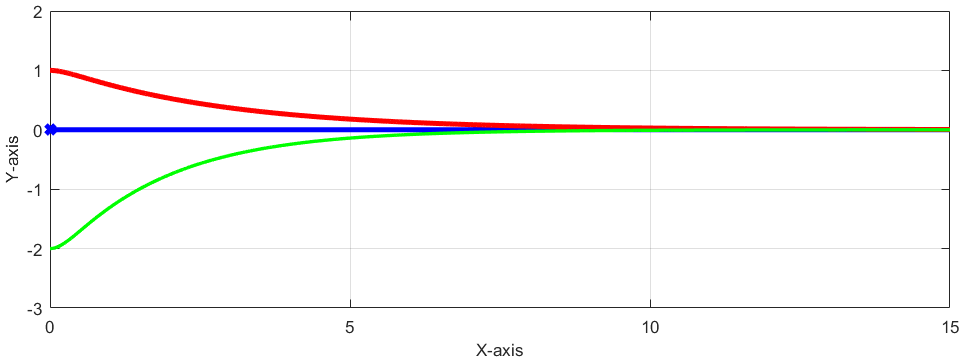
先の条件１の場合と同様に、車の位置（緑線）が徐々に目標軌跡（青線）に近づいていることが分かります。

 

また、条件１（赤線）と条件２（緑線）を比較すると、条件２の方が条件１よりも大きく目標軌跡（青線）からずれているのに、早く目標軌跡に近づいていることが分かります。

 

これは、ハンドルの角度\(\phi\)を算出するために用いている距離\(d\)によるもので、この距離\(d\)を制御することで目標軌跡に到達する時間をコントロールすることが出来ます。

 

まとめ

今回は、実際に車やロボットの自動運転を行うために、自動運転モデルの問題を少し簡単化して、実際に車を制御する方法を紹介しました。

 

今回紹介した方法を用いることで、車の現在位置と目標軌跡との誤差からハンドルの角度を算出し、車を目標軌跡に近づけることが出来ます。

 

次回は、新たに比例定数を用いて自動運転車の制御を行う方法を紹介したいと思います。

自動運転車を制御してみよう：実際に簡単な制御をしてみる 本シリーズは、車やロボットの自動運転を実現するために、必要となる制御工学の情報を紹介しています。 https://taji...

 

合わせて読みたい

実際にシミュレーションに用いたMATLABコードを紹介しています。

自動運転車を制御するプログラムの紹介 本シリーズでは、車やロボットの自動運転を実際に行うために必要となる制御工学の情報を紹介していきます。 https://ta...