複数の質量からなるモデルについて、固有値解析を用いて運動方程式からシステムの振動を算出する方法を紹介します。
ラプラス変換を用いて、運動方程式からシステムの振動を算出する方法はこちらの記事を参考にしてください。
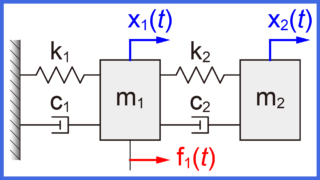
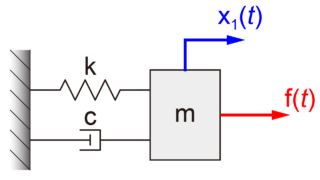
2質量モデルの運動方程式
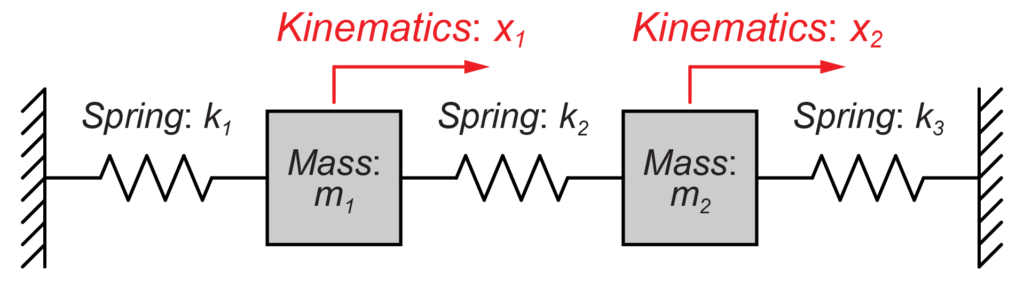
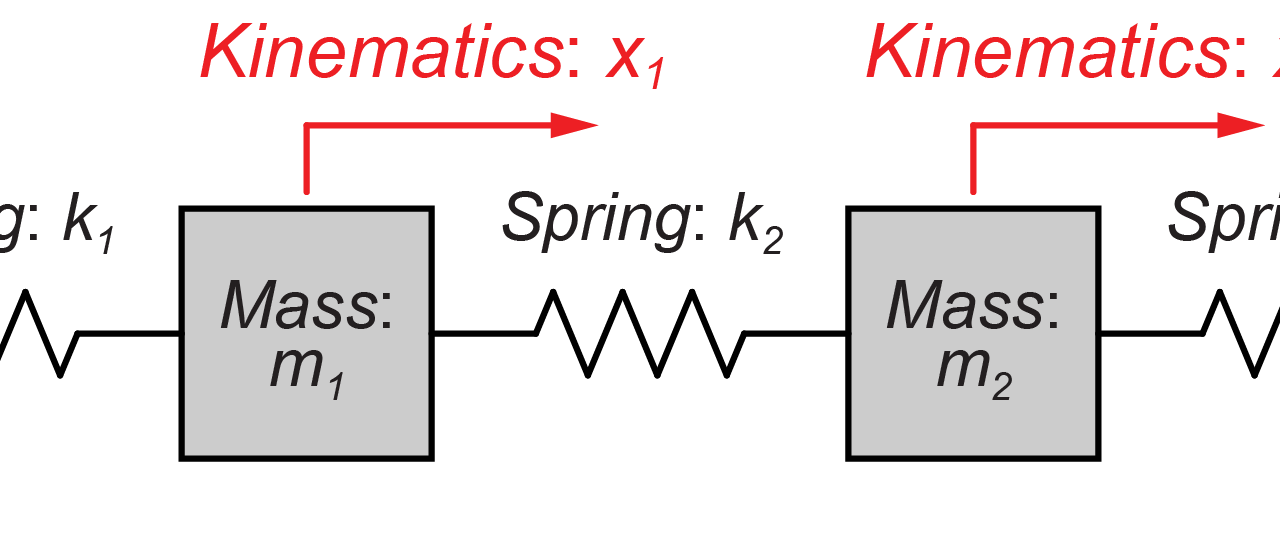
図のように2つの質量(m1とm2)が、それぞればね(k1、k2、k3)によって壁と互いに接続されているモデルを扱います。
各パラメータについて、
$$ \begin{eqnarray} \left\{ \begin{array}{l} m_1 = m_2 = m \\ k_1 = k_2 = k_3 = k \end{array} \right. \end{eqnarray} $$
とすると、この2質量モデルの運動方程式は、
$$ \begin{eqnarray} \left\{ \begin{array}{l} m \ddot{x}_1(t) + 2 k x_1(t) – k x_2(t) = 0 \\ m \ddot{x}_2(t) – k x_1(t) + 2 k x_2(t) = 0 \end{array} \right. \end{eqnarray} $$
となります。
詳しくは、こちらの記事を参考にしてください。

このシステムについて、初期条件として時刻t=0において、
$$ \begin{eqnarray} \left\{ \begin{array}{l} x_1(0) = 0 \\ x_2(0) = 1 \\ \dot{x}_1(0) = \dot{x}_2(0) = 0 \end{array} \right. \end{eqnarray} $$
とした時のシステムの振動の様子を固有値解析手法を用いて算出していきます。
システムの固有値を求める
今回のシステムについて、各質量の変位を
$$ \begin{eqnarray} x_1(t) &=& A_1 \sin \left(\omega t \right) \\ x_2(t) &=& A_2 \sin \left(\omega t \right) \end{eqnarray} $$
と置きます。
ここで、
$$ \omega_n = \sqrt{\frac{k}{m}} $$
として、変位x1(t)とx2(t)をシステムの運動方程式に代入すると、
$$ \begin{eqnarray} && \left\{ \begin{array}{l} \ddot{x}_1(t) + 2 {\omega_n}^2 x_1(t) – {\omega_n}^2 x_2(t) = 0 \\ \ddot{x}_2(t) – {\omega_n}^2 x_1(t) + 2 {\omega_n}^2 x_2(t) = 0 \end{array} \right. \\ && \Rightarrow \left\{ \begin{array}{l} – A_1 \omega^2 \sin \left(\omega t \right) + 2 {\omega_n}^2 A_1 \sin \left(\omega t \right) – {\omega_n}^2 A_2 \sin \left(\omega t \right) = 0 \\ – A_2 \omega^2 \sin \left(\omega t \right) – {\omega_n}^2 A_1 \sin \left(\omega t \right) + 2 {\omega_n}^2 A_2 \sin \left(\omega t \right) = 0 \end{array} \right. \\ && \Rightarrow \left\{ \begin{array}{l} A_1 \left( 2 {\omega_n}^2 – \omega^2 \right) + A_2 \left(-{\omega_n}^2 \right) = 0 \\ A_1 \left(-{\omega_n}^2 \right) + A_1 \left( 2 {\omega_n}^2 – \omega^2 \right) = 0 \end{array} \right. \end{eqnarray} $$
となります。
この連立方程式を行列式に書き換えると、
$$ \begin{bmatrix} 2 {\omega_n}^2 – \omega^2 & -{\omega_n}^2 \\ -{\omega_n}^2 & 2 {\omega_n}^2 – \omega^2 \end{bmatrix} \begin{bmatrix} A_1 \\ A_2 \end{bmatrix} = \begin{bmatrix} 0 \\ 0 \end{bmatrix} $$
となります。
ここで右辺が0なので、左辺も0になるためには、どちらかの行列が0でなければなりません。
A1とA2は、最初に置いた変位の振幅なので0ではないとすると、
$$ \begin{vmatrix} 2 {\omega_n}^2 – \omega^2 & -{\omega_n}^2 \\ -{\omega_n}^2 & 2 {\omega_n}^2 – \omega^2 \end{vmatrix} = 0$$
となる必要があります。
これより、
$$ \begin{eqnarray} \left(2 {\omega_n}^2 – \omega^2\right)^2 – {\omega_n}^4 &=& 0 \\ \omega^4 -4 {\omega_n}^2 – 3 {\omega_n}^2 &=& 0 \\ \left(\omega^2 – {\omega_n}^2 \right) \left(\omega^2 – 3 {\omega_n}^2 \right) &=& 0 \\ \omega^2 &=& {\omega_n}^2 , 3 {\omega_n}^2 \end{eqnarray}$$
と求めることが出来ます。
よって、このシステムの振動は、
$$ \begin{eqnarray} \left\{ \begin{array}{l} \omega_1 &=& \omega_n \\ \omega_2 &=& \sqrt{3} \omega_n \end{array} \right. \end{eqnarray} $$
の2つの周波数の合成関数で表すことが出来ると分かります。
まとめ
今回は、2質量モデルの運動方程式からシステムの振動の様子を固有値解析を用いて算出する方法を紹介しました。
今回求めた結果は、以前の記事内でラプラス変換を用いて求めた結果と同じになります。

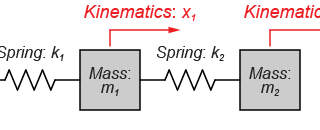




 ELEGOO Arduinoスターターキット
ELEGOO Arduinoスターターキット

 UNO R3スマートロボットカー
UNO R3スマートロボットカー

 Raspberry Pi 3 Model b+
Raspberry Pi 3 Model b+
