前回の記事では、詳細な根軌跡を描くために必要となる情報として、実軸上から軌跡が分岐する点を求める方法を紹介しました。
今回は、他の詳細な根軌跡を書くための情報として、軌跡と虚軸との交点を求める方法を紹介します。
詳細な根軌跡を描くための情報
より詳細な根軌跡を書くために必要となる情報として、
- 実軸上からの分岐点
- 虚軸との交点 ← 今回
- 複素数点への入出力角
があります。
今回は、２つ目の軌跡が虚軸と交差する点を求める方法を紹介します。
フィードバックシステムと虚軸との交点
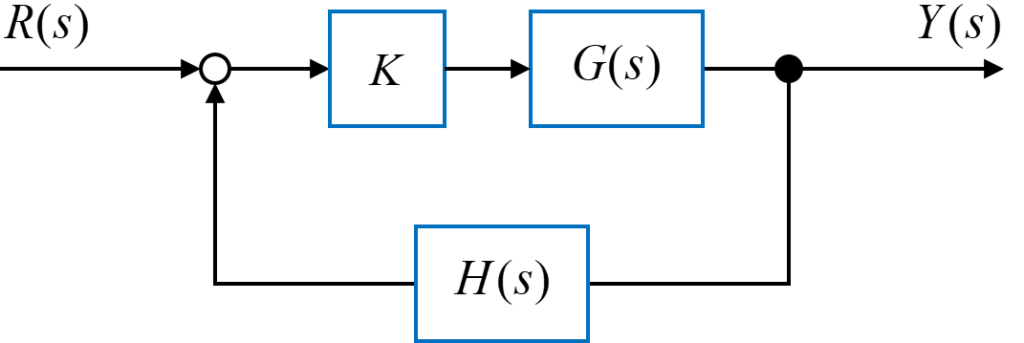
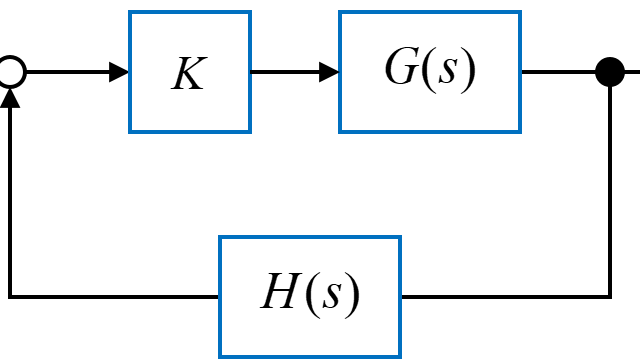
図のようなフィードバックシステムの開ループ伝達関数が
$$ K G(s) H(s) = \frac{K}{(s+1)(s+2)(s+4)} $$
で与えられるシステムについての根軌跡を考えます。
以前の記事で紹介した根軌跡のルールを用いることで、今回のフィードバックシステムの根軌跡の概略を描くことが出来ます。
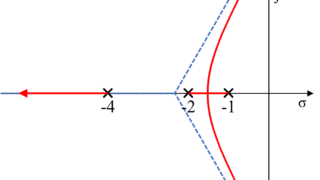
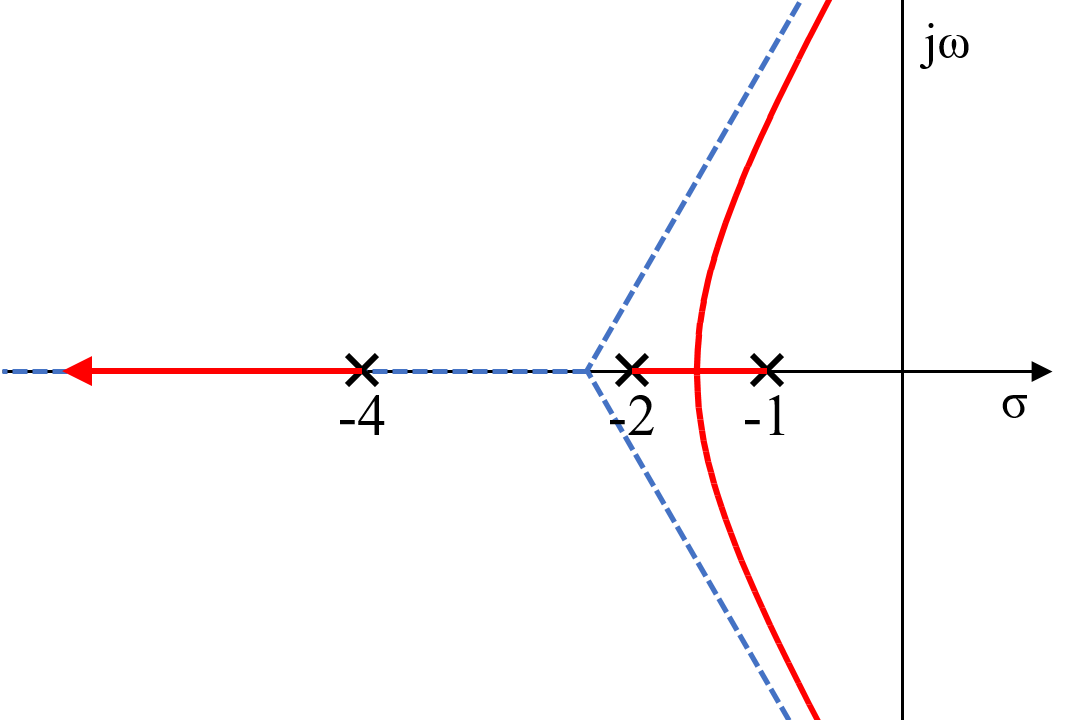
開ループ伝達関数の極\(-1\)と\(-2\)を始点とした軌跡が実軸上で合わさり、ある点で上下方向に分岐されます。
この分岐した軌跡は、算出される漸近線に沿って虚数軸と交わります。
この虚数軸と交差する点を求めていきます。
虚数軸との交点を算出する
根軌跡で表されるフィードバックシステムの閉ループ伝達関数の極の位置が虚数軸と交わる点は、ラウス・フルビッツの安定判別法を用いて求めることが出来ます。
ラウス・フルビッツの安定判別法については、こちらの記事を参考にしてください。
閉ループ伝達関数の極の位置が虚数軸上にあるということは、このシステムは安定限界にあるということを意味します。
ラウス・フルビッツの安定判別法を用いることで、システムが安定性を保つことが出来る限界の点を求めることが出来ます。
よって、ラウス・フルビッツの安定判別法で用いるラウス配列より、システムが安定性を保つことが出来る限界点、つまり安定限界となるゲイン\(K\)を算出し、その値を用いて根軌跡上の軌跡が虚軸と交わる点を求めていきます。
実際に軌跡と虚軸との交点を算出する
今回用いるフィードバックシステムの閉ループ伝達関数\(T(s)\)の分母より得られる特性方程式\(D(s)\)は、開ループ伝達関数
$$ K G(s) H(s) = \frac{K}{(s+1)(s+2)(s+4)} $$
より、
$$ D(s) = (s+1)(s+2)(s+4) + K $$
$$ = s^3 + 7 s^2 + 14 s + 8+K $$
となります。
この特性方程式\(D(s)\)より、ラウス配列を求めていきます。
$$ \begin{eqnarray} \begin{array}{c|ccc} s^3 & 1 & 14 & 0 \\ s^2 & 7 & 8+K & 0 \\ s^1 & \frac{7\cdot14-1\cdot(8+K)}{7}=\frac{90-K}{7} & 0 & \\ s^0 & 8+K & & \\ \end{array} \end{eqnarray} $$
もとめたラウス配列より、ゲイン\(K\)が正の数だとすると、
$$ K = 90 $$
の時に、システムは安定限界になる事が分かります。
このゲイン\(K\)の値と\(s^2\)の行より、
$$ 7 s^2 + (8+K) = 0 $$
$$ \Rightarrow 7 s^2 + 98 = 0 $$
という関係式が導かれます。
よって、この関係式より
$$ s = \pm \sqrt{-\frac{98}{7}} = \pm \sqrt{-14} $$
$$ \Rightarrow s = \pm j 3.742 $$
となります。
これらより、今回のフィードバックシステムの根軌跡は、ゲイン\(K=90\)の時に\(\pm j 3.742\)の点で虚数軸と交わることが分かりました。
まとめ
今回は、より詳細な根軌跡を書くために必要となる情報として、根軌跡で表される軌跡と虚数軸とが交わる点を求める方法を紹介しました。
次回は、残りの根軌跡を詳細に書くための情報として、複素数で表される極及び零点の入出力角を算出する方法を紹介したいと思います。
ELEGOO Arduinoスターターキット
UNO R3スマートロボットカー
Raspberry Pi 3 Model b+
