伝達関数で表されたロボットや工作機械などのシステムのボード線図を書く方法を紹介しています。
前回までの記事では、システムの伝達関数を要素ごとに分割し、各要素についてボード線図を求めました。
今回は、求めた各要素のボード線図を足し合わせることで、システム全体のボード線図を書いていきます。
伝達関数と各要素のボード線図
前々回からの続きとして、伝達関数\(G(s)\)
$$ G(s) = \frac{4(s+5)}{s (s+0.2) (s+10)} $$
が与えられた場合のボード線図を求めていきます。

この伝達関数\(G(s)\)を
$$ G(s) = \frac{10 (\frac{s}{5}+1)}{s (5 s+1) (\frac{s}{10}+1)} $$
と変換し、この変換した伝達関数\(G(s)\)を構成する要素
- 比例要素:\(10\)
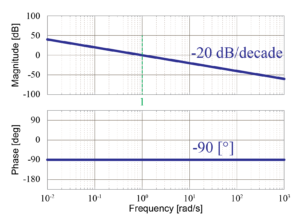
- 積分要素:\(\frac{1}{s}\)
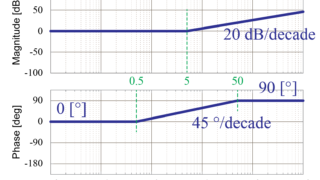
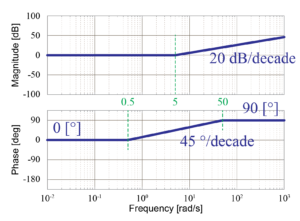
- 1次進み要素:\(\frac{s}{5}+1\)
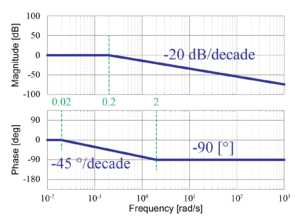
- 1次遅れ要素:\(\frac{1}{5s+1}\)、\(\frac{1}{\frac{s}{10}+1}\)
について、各要素のボード線図を足し合わせることで、システム全体のボード線図を求めていきます。
前回の記事では、この各要素についてボード線図を求めました。


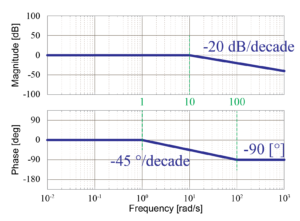
今回は、これら各要素のボード線図を1つに足し合わせていきます。
伝達関数を足し合わせる
伝達関数\(G(s)\)をボード線図を求めるために、伝達関数\(G(s)\)を構成する要素
- 比例要素:\(10\)
- 積分要素:\(\frac{1}{s}\)
- 1次進み要素:\(\frac{s}{5}+1\)
- 1次遅れ要素:\(\frac{1}{5s+1}\)、\(\frac{1}{\frac{s}{10}+1}\)
のゲイン線図と位相線図をそれぞれ足し合わせていきます。
ゲイン線図
各要素のゲイン線図を同じグラフ上に重ねると下図のようになります。
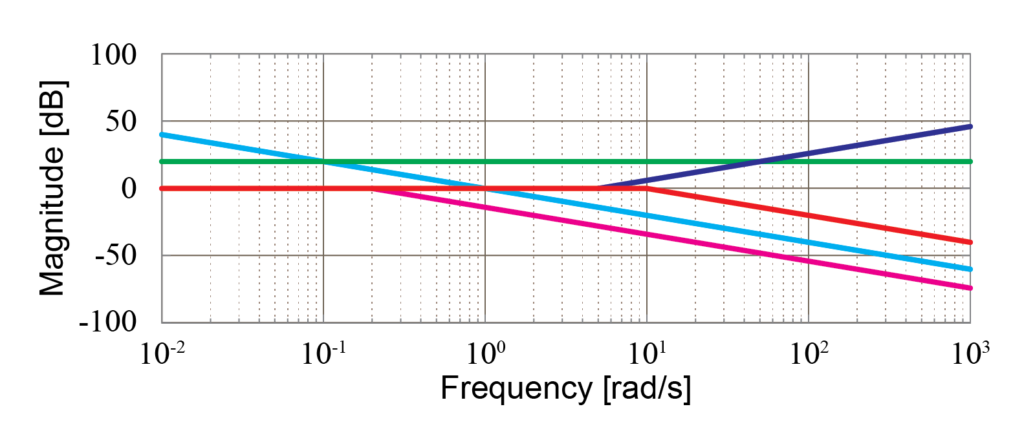
ここで、比例要素\(10\)は緑線、積分要素\(\frac{1}{s}\)は水色線、1次進み要素\(\frac{s}{5}+1\)は青線、そして1次遅れ要素の内\(\frac{1}{5s+1}\)は紫線、\(\frac{1}{\frac{s}{10}+1}\)は赤線で示しています。
まず、周波数\(\omega\)が0.2[rad/sec]までは比例要素(緑線)と積分要素(水色線)のみがゲイン値を持ちます。
よって、足し合わせたゲイン値は積分要素の値を比例要素の分(20dB)上にずらした-20[dB/decade]の傾きの直線になります。
そして、周波数\(\omega\)が0.2[rad/sec]から1つ目の1次遅れ要素(紫線)の影響より、足し合わせたゲイン値は傾きが-40[dB/decade]の直線となります。
この足し合わされた直線は、周波数\(\omega\)が5[rad/sec]から1次進み要素(青線)の影響より傾きが-20[dB/decade]と変わります。
そして、周波数\(\omega\)が10[rad/sec]より2つ目の1次遅れ要素(赤線)により傾きが-40[dB/decade]の直線で表されます。
よって、システム全体のゲイン線図は下図のように求めることが出来ます。
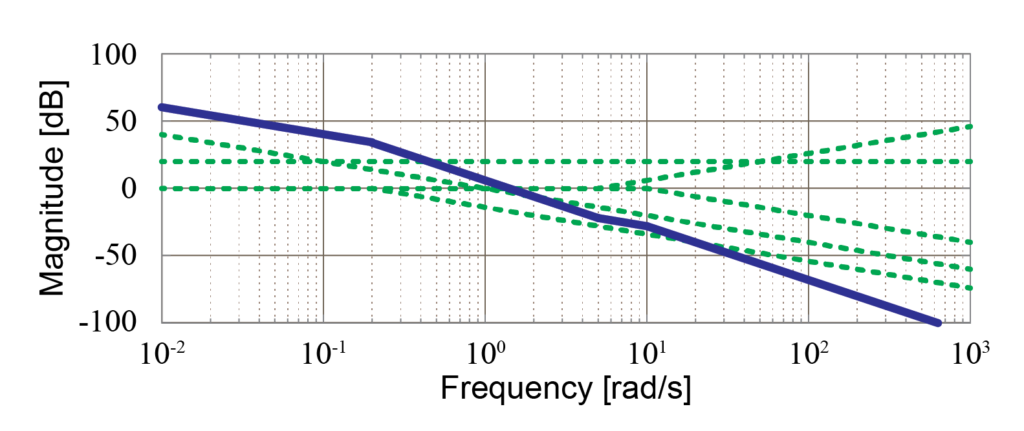
各要素のゲイン線図(緑の点線)を足し合わせることで、システム全体のゲイン線図(青の実線)を求めることが出来ました。
位相線図
ゲイン線図と同様に、位相線図についても各要素の位相線図を足し合わせることで全体の位相線図を求めていきます。
各要素の位相線図を同じグラフ上にまとめると下図のように表せます。
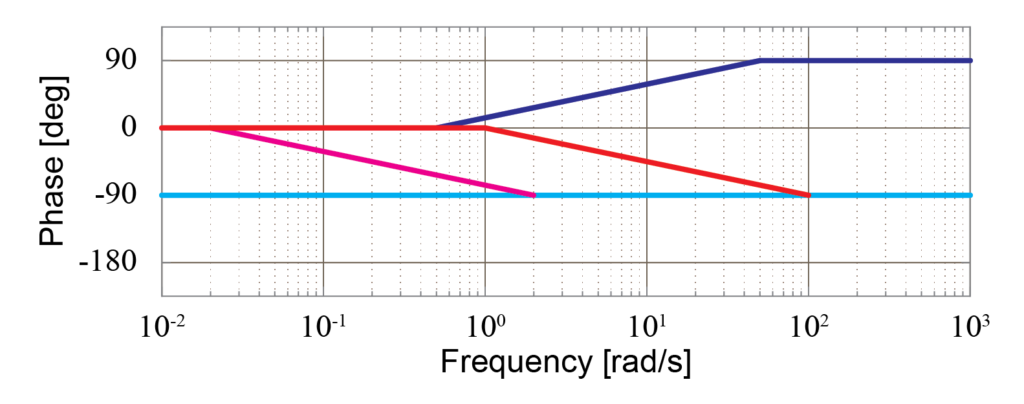
ここで、積分要素\(\frac{1}{s}\)は水色線、1次進み要素\(\frac{s}{5}+1\)は青線、そして1次遅れ要素の内\(\frac{1}{5s+1}\)は紫線、\(\frac{1}{\frac{s}{10}+1}\)は赤線で示しています。
また、比例要素\(10\)について位相線図は常に0dBで一定なので省略しています。
これら各要素について求められた位相線図を足し合わせた結果、システム全体の位相線図は下図のように求めることが出来ます。
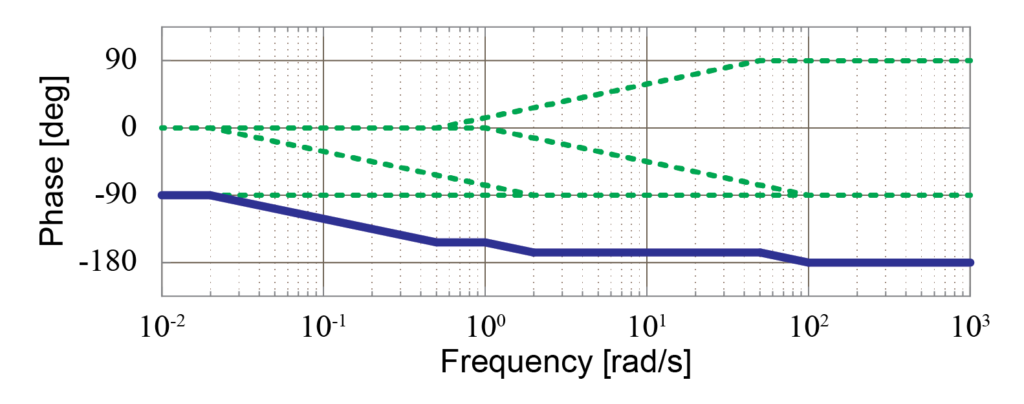
ゲイン線図の場合と同様に、各要素の位相線図(緑の点線)を足し合わせて、システム全体の位相線図(青の実線)を求めることが出来ました。
実際のボード線図と比較
先ほど求めたボード線図は漸近線を用いた近似で表したものです。
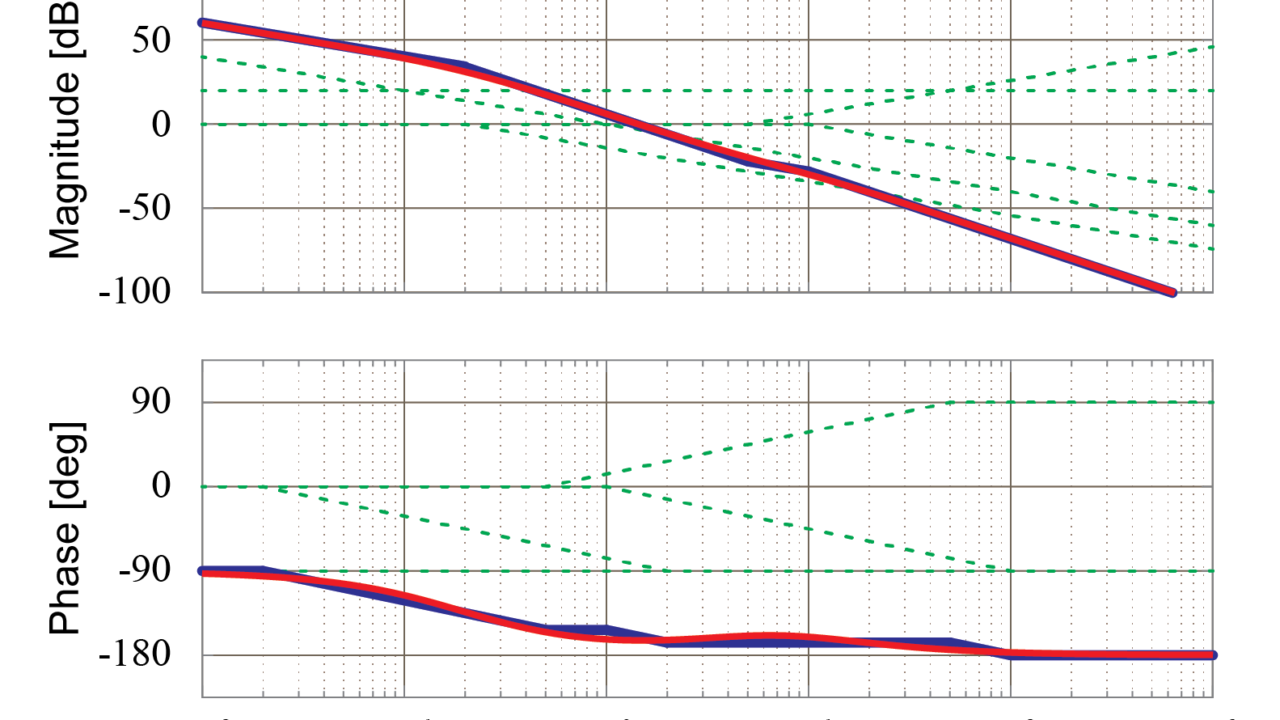
そこで、求めた漸近線近似によるボード線図と実際のシミュレーションにより求めたボード線図とを比較してみます。
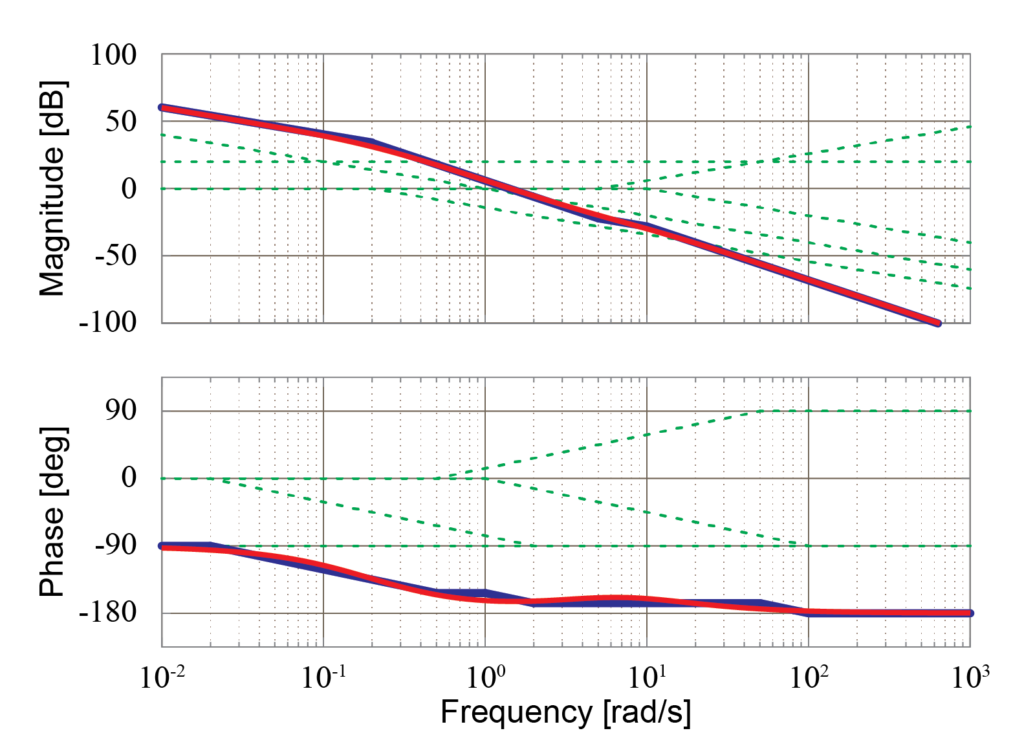
実際に比較した結果、漸近線近似により求められたボード線図(青線)はシミュレーションによる結果(赤線)とほぼ同一になっていることが分かります。
これより、今回紹介してきた方法を用いることで、複雑なシステムのボード線図を実際に書けることが分かりました。
まとめ
今回は、システムの伝達関数を構成する各要素のボード線図を足し合わせることで、システム全体のボード線図を求める方法を紹介しました。
与えられた伝達関数から直接ボード線図を書くことは難しいですが、伝達関数を要素ごとに分割した後に足し合わせることで、比較的簡単にボード線図を書くことが出来ます。


























 ELEGOO Arduinoスターターキット
ELEGOO Arduinoスターターキット

 UNO R3スマートロボットカー
UNO R3スマートロボットカー

 Raspberry Pi 3 Model b+
Raspberry Pi 3 Model b+
