連続的な線形システムの安定性を確認する方法：制御工学入門

本シリーズでは、制御工学で学ぶ基本的な知識から実際の応用例までを、なるべく分かりやすく解説しています。

制御工学入門制御工学（Control Engineering）についての情報を紹介します。動的システムと制御方法世の中にあふれる動的...

前回までの記事では、常微分方程式で表された線形システムを固有値と固有ベクトルを用いて解く方法を紹介しました。

今回は、この線形システムの動作が安定なのか、それとも不安定なのかを確認する方法を紹介していきたいと思います。

Contents

線形システムの安定性とは
システムの安定性を確認する
実際に安定性を確認してみた
まとめ

線形システムの安定性とは

システムの安定性を確認することはとても重要です。

前回までの記事で、線形システムの常微分方程式

$$ \dot{\boldsymbol{ x }} = \boldsymbol{ A } \boldsymbol{ x } $$

について、行列Aの固有値λと固有ベクトルζを用いて座標系を変換することで

$$ \boldsymbol{ x } (t) = \boldsymbol{ T } e^{\boldsymbol{ D } t} \boldsymbol{ T }^{-1} \boldsymbol{ x } (0) $$

と簡単に解く方法を紹介しました。

今回は、この線形システムの解x(t)の安定性（Stability）について考えます。

この安定性を調べる方法として、時間の経過とともに解x(t)の値が

無限大に発散するのか？
0に収束するのか？
それとも何か違う動きをするのか？

を確認します。

そして、解x(t)の値が時間の経過とともに0に収束した場合、このシステムは安定であると言えます。

安定性を確認する方法は、簡単な方法から難しい方法まで様々な手法があります。

今回は、シンプルで簡単な手法について紹介します。

システムの安定性を確認する

線形システムの一般解x(t)を求める式

$$ \boldsymbol{ x } (t) = \boldsymbol{ T } e^{\boldsymbol{ D } t} \boldsymbol{ T }^{-1} \boldsymbol{ x } (0) $$

に含まれるにe^Dtついて

$$ e^{\boldsymbol{ D } t} = \begin{bmatrix} e^{\lambda_1 t} & & & & 0 \\ & e^{\lambda_2 t} & & & \\ & & e^{\lambda_3 t} & & \\ & & & \ddots & \\ 0 & & & & e^{\lambda_n t} \end{bmatrix} $$

に含まれるe^λtの内、一つでも無限大に発散することがあれば、それは

$$ \boldsymbol{ x } (t) = \boldsymbol{ T } e^{\boldsymbol{ D } t} \boldsymbol{ T }^{-1} \boldsymbol{ x } (0) $$

が無限大になる可能性があるということです。

固有値λについて

$$ \lambda = a + i b $$

と実数aとbを使って複素数で表したとき、e^λtはオイラーの公式（Euler’s Formula）を用いて

$$ e^{\lambda t} = e^{a t} \left( \cos (b t) + i \sin (b t) \right) $$

のように表すことが出来ます。

ここで、三角関数のsin(bt)とcos(bt)の大きさは最大でも1です。

よって、残りのe^atにより、e^λtが無限大に発散するかが分かります。

e^atの式からも分かるように、

a > 0のとき、 e^atは無限大に発散
a < 0のとき、 e^atは0に収束

となります。

これより、すべての固有値λの実部がマイナスであれば、システムは安定になります。

言い換えると、一つでも実部がプラスの固有値λが存在すれば、システムは不安定になります。

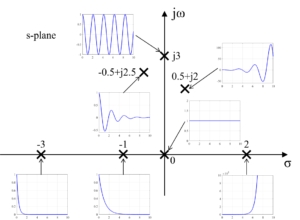
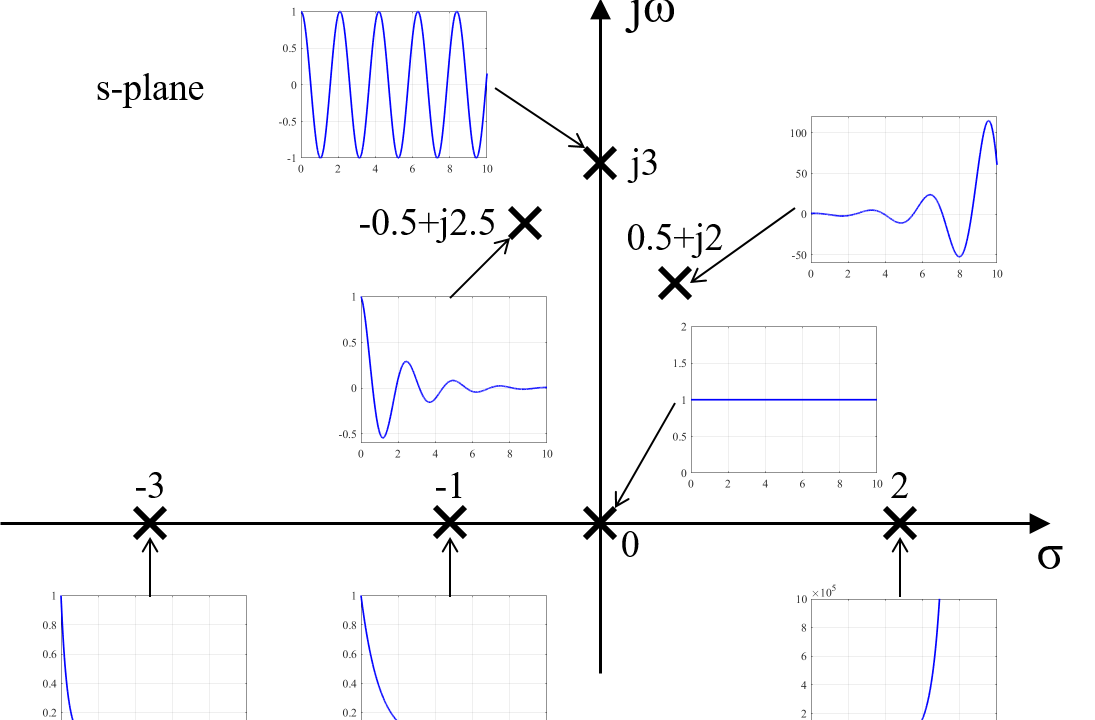
この図は、複素数で与えられた固有値λ=σ+jωの複素平面上での位置と、その固有値λを用いた応答e^λtの様子を表しています。

図からも分かるように、複素平面において左側に固有値がある場合（複素数の実部がマイナスの場合）は安定で、右側にある場合（実部がプラスの場合）は応答が発散するため不安定になります。

実際に安定性を確認してみた

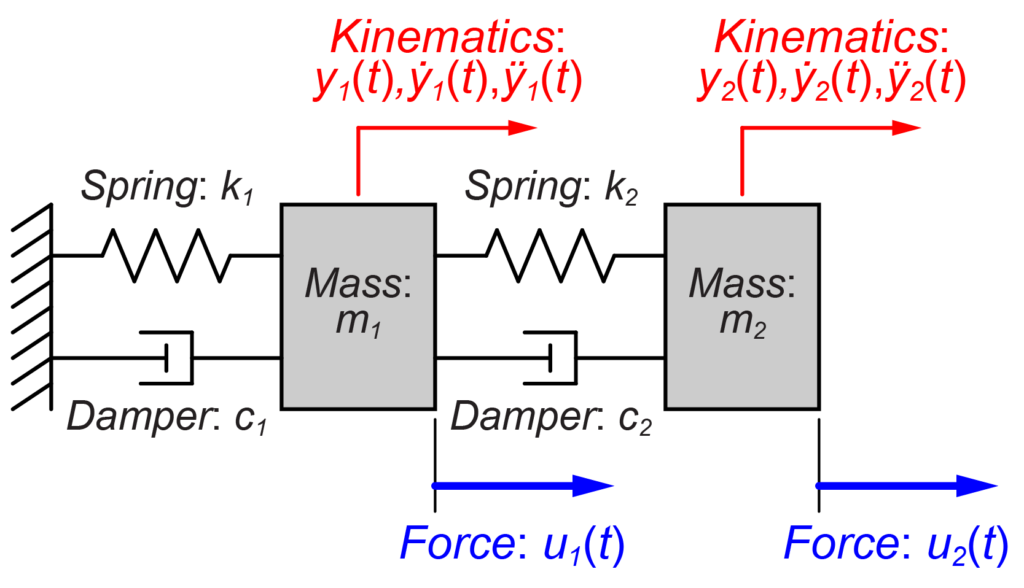
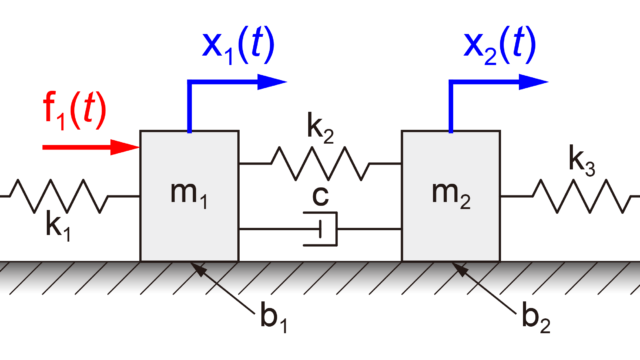
以前の記事で取り扱った、２つの質量がそれぞれバネとダンパーで接続されたモデルについて、今回紹介した方法で安定性を確認してみます。

以前の記事より、このモデルの

$$ \dot{\boldsymbol{ x }} = \boldsymbol{ A } \boldsymbol{ x } $$

に含まれる行列Aの固有値λは

$$ \begin{eqnarray} \left\{ \begin{array}{l} \lambda_1 = -0.7891+0.5368i \\ \lambda_2 = -0.7891-0.5368i \\ \lambda_3 = -0.2109+0.4680i \\ \lambda_4 = -0.2109-0.4680i \end{array} \right. \end{eqnarray} $$

の4つです。

行列Aと固有値λの求め方について、詳しくはこちらの記事を参考にしてください。