ロボットをスムーズに制御するために、台形速度プロファイルを用いた手法があります。
以前の記事では、この加速度を制限した台形速度手法について、利点と計算式について紹介しました。
今回の記事では、実際に具体的な値を用いて計算を行うことで、より台形速度制御を行うための軌跡生成について理解を深めていきたいと思います。
加速度制限台形速度制御とは
加速度制限台形速度制御とは、軌跡生成に用いる加速度の値を制限することで、スムーズな台形の速度プロファイルを作成し制御する方法です。
台形速度プロファイル
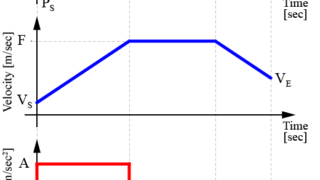
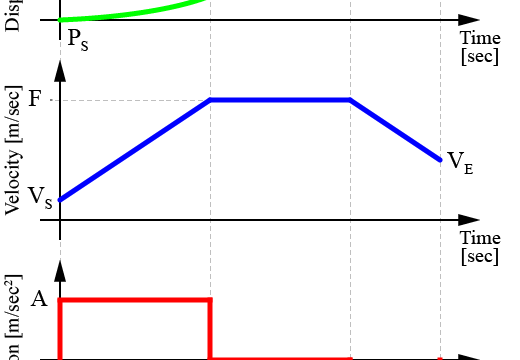
加速度制限台形速度制御で用いられる台形速度プロファイルは、下の図のように表されます。
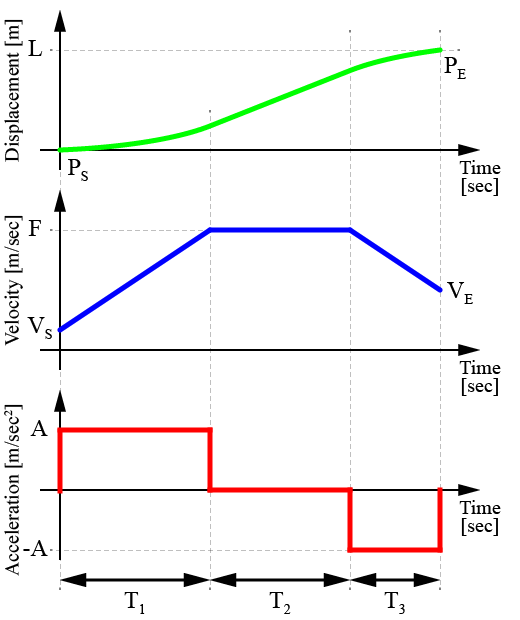
台形速度プロファイルは、全部で3つの期間
- 加速期間(T1)
- 巡航期間(T2)
- 減速期間(T3)
で生成されています。
この台形速度プロファイルを作成するため、必要となるパラメータ(T1、T2、T3)を求めます。
パラメータの算出
ロボットの初速VSから終速VEまでを結ぶスムーズな速度プロファイルを作成ためのパラメータ(T1、T2、T3)を算出方法を紹介します。
ロボットの巡航速度をF[m/sec]とし、加速度をA[m/sec2]としたときの加速期間T1と減速期間T3は
$$ \begin{eqnarray} T_1 &=& \frac{F – V_S}{A} \\ T_3 &=& \frac{F – V_E}{A} \end{eqnarray} $$
で求めることが出来ます。
この加速期間T1と減速期間T3で移動する距離(L1とL3)は
$$ \begin{eqnarray} L_1 &=& \frac{1}{2}(V_S+F) T_1 \\ L_3 &=& \frac{1}{2}(F+V_E) {T_3} \end{eqnarray}$$
と求められるため、ロボットの移動距離をLとすると巡航期間T2は
$$ T_2 = \frac{L – L_1 – L_3}{F} $$
で算出することが出来ます。
詳しくは、こちらの記事を参考にしてください。

実際に台形速度制御を行う
最大速度と最大加速度が5[m/sec]と4[m/sec2]の時に、停止状態(速度0[m/sec])のロボットが10[m]進んだ後に速度2[m/sec]の状態になるような軌跡生成を行います。
よって、今回の記事で求める台形速度プロファイルの条件は
$$ \begin{eqnarray} \left\{ \begin{array}{l} L = 10 \ [m] \\ F = 5 \ [m/sec] \\ A = 4 \ [m/{sec}^2] \end{array} \right. \end{eqnarray} $$
と
$$ \begin{eqnarray} \left\{ \begin{array}{l} V_S = 0 \ [m/sec] \\ V_E = 2 \ [m/sec] \end{array} \right. \end{eqnarray} $$
になります。
これらの条件値を用いて、台形速度プロファイルの作成に必要となるパラメータの算出をしていきます。
加速期間T1の算出
まずはじめに、加速期間T1を求めていきます。
ロボットの巡航速度と加速度がF[m/sec]とA[m/sec2]、初速がVS[m/sec]のときの加速期間T1は
$$ T_1 = \frac{F – V_S}{A} $$
で求めることが出来ます。
よって、この式に今回の条件
$$ \begin{eqnarray} \left\{ \begin{array}{l} F = 5 \ [m/sec] \\ A = 4 \ [m/{sec}^2] \\ V_S = 0 \end{array} \right. \end{eqnarray} $$
を代入すると、軌跡生成に必要となる加速期間T1は
$$ \begin{eqnarray} T_1 &=& \frac{F – V_S}{A} \\ &=& \frac{5 – 0}{4} \\ &=& 1.25 \ [sec] \end{eqnarray} $$
と算出することが出来ます。
減速期間T3の算出
加速期間T1の場合と同様に減速期間T3を求めていきます。
ロボットの巡航速度と加速度がF[m/sec]とA[m/sec2]、終速がVE[m/sec]のときの減速期間T3は
$$ T_3 = \frac{F – V_E}{A} $$
で求めることが出来ます。
よって、この式に今回の条件
$$ \begin{eqnarray} \left\{ \begin{array}{l} F = 5 \ [m/sec] \\ A = 4 \ [m/{sec}^2] \\ V_E = 2 \end{array} \right. \end{eqnarray} $$
を代入すると、軌跡生成に必要となる加速期間T1は
$$ \begin{eqnarray} T_1 &=& \frac{F – V_E}{A} \\ &=& \frac{5 – 2}{4} \\ &=& 0.75 \ [sec] \end{eqnarray} $$
と算出することが出来ます。
巡航期間T2の算出
最後に、巡航期間T2を求めていきます。
先に求めた加速期間T1と減速期間T3で移動する距離L1とL3は、
$$ \begin{eqnarray} L_1 &=& \frac{1}{2}(V_S+F) T_1 \\ L_3 &=& \frac{1}{2}(F+V_E) {T_3} \end{eqnarray}$$
で求めることが出来ます。
よって、この式に今回の条件
$$ \begin{eqnarray} \left\{ \begin{array}{l} F = 5 \ [m/sec] \\ A = 4 \ [m/{sec}^2] \\ V_S = 0 \\ V_E = 2 \end{array} \right. \end{eqnarray} $$
を代入すると、加速期間T1と減速期間T3での移動距離L1とL3はそれぞれ
$$ \begin{eqnarray} L_1 &=& \frac{1}{2}(V_S+F) T_1 \\ &=& \frac{1}{2}(0+5) 1.25 \\ &=& 3.125 \ [m] \end{eqnarray} $$
と
$$ \begin{eqnarray} L_3 &=& \frac{1}{2}(F+V_E) T_3 \\ &=& \frac{1}{2}(5+2) 0.75 \\ &=& 2.625 \ [m] \end{eqnarray} $$
のように求めることが出来ます。
巡航期間T2は、ロボットの移動距離をL、加速期間T1と減速期間T3での移動距離をそれぞれL1とL3とすると
$$ T_2 = \frac{L – L_1 – L_3}{F} $$
で算出することが出来るため、この式に今回の条件(FとL)と求めた値(L1とL3)
$$ \begin{eqnarray} \left\{ \begin{array}{l} F = 5 \ [m/sec] \\ L = 10 \ [m] \\ L_1 = 3.125 \ [m] \\ L_3 = 2.625 \ [m] \end{array} \right. \end{eqnarray} $$
を代入することで、
$$ \begin{eqnarray} T_2 &=& \frac{L – L_1 – L_3}{F} \\ &=& \frac{10 – 3.125 – 2.625}{5} \\ &=& 0.85 \ [sec] \end{eqnarray} $$
と算出することが出来ました。
台形速度制御を行った結果
算出したパラメータ
$$ \begin{eqnarray} \left\{ \begin{array}{l} T_1 = 1.25 \ [sec] \\ T_2 = 0.85 \ [sec] \\ T_3 = 0.75 \ [sec] \end{array} \right. \end{eqnarray} $$
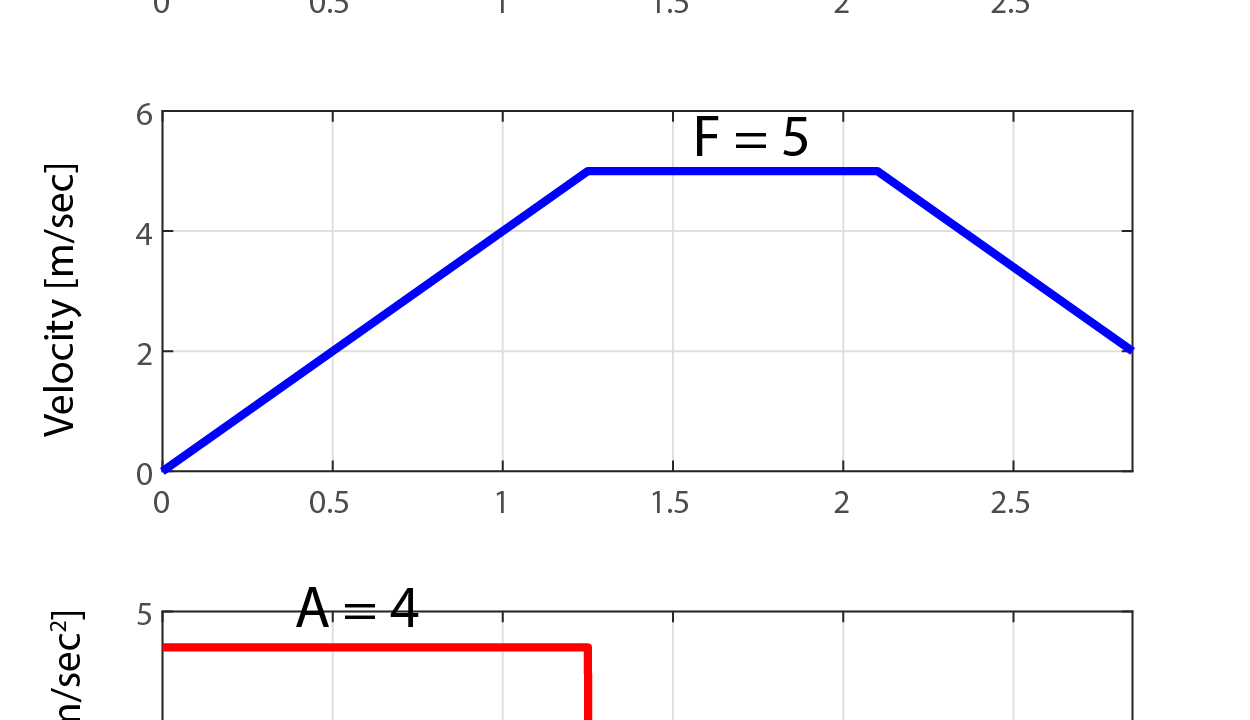
を基に、台形速度プロファイルを生成した結果は下の図の通りです。
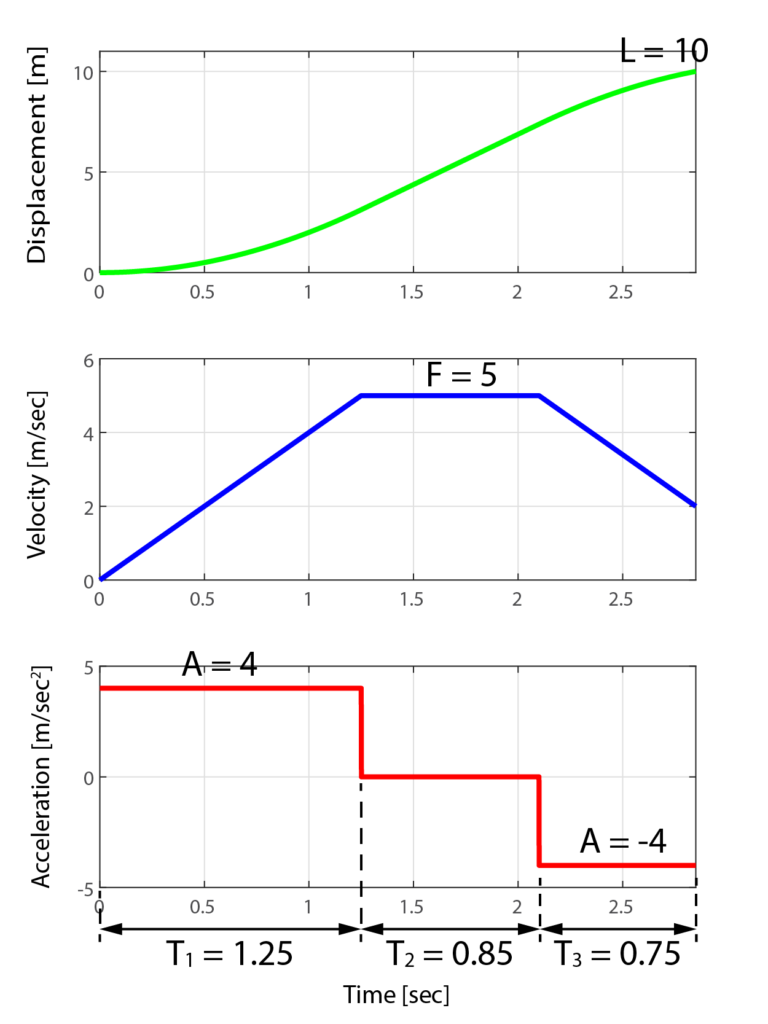
生成した台形速度制御の軌跡を見ると分かるように、台形速度プロファイルの3つの期間はそれぞれ算出したパラメータ(T1、T2、T3)の値になっています。
そして、加速期間と減速期間の加速度は、条件で与えられた最大加速度の4[m/sec2]と-4[m/sec2]を用いています。
さらに巡航期間の速度も、条件で与えられた最大速度の5[m/sec]を用いています。
これより、今回紹介した軌跡生成手法は最大速度および最大加速度を用いていることから、時間最適(Time-optimal)のスムーズな台形速度プロファイルを生成できることが分かりました。
与えられた条件によって、各期間の計算結果が0や負の値になる場合があります。
その場合には、今回紹介した計算手法とは異なる方法を用いる必要があります。
まとめ
今回は、ロボットをスムーズに動作させるために用いられている台形速度制御について、実際に具体的な値を用いて速度プロファイルを求める流れを紹介しました。
次回は、記事内で注意点として紹介した各期間の値が正の値でない場合(0や負の値の場合)niについて、加速度制限を用いて台形速度制御を行うための軌跡生成手法を紹介したいと思います。

























 ELEGOO Arduinoスターターキット
ELEGOO Arduinoスターターキット

 UNO R3スマートロボットカー
UNO R3スマートロボットカー

 Raspberry Pi 3 Model b+
Raspberry Pi 3 Model b+
