ブロック線図を簡略化する：内部信号を用いる方法（その２）

前回からの続きとして、複雑なブロック線図を内部信号を用いて簡略化（簡単化）して、１つにまとめる方法を紹介しています。

前回の記事では、定義した内部信号と入出力信号の関係式を求めました。

ブロック線図を簡略化する：内部信号を用いる方法（その１）複雑なブロック線図を簡略化（簡単化）して、１つにまとめる方法を紹介します。ロボットなど制御システムをブロック線図...

今回は、算出した関係式から実際にブロック線図を簡略化して１つの伝達要素を求めるする方法を紹介します。

Contents

取り扱うブロック線図
連立方程式を解く
まとめ

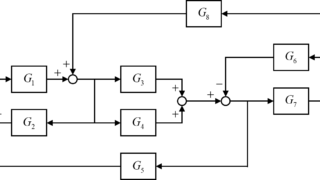
取り扱うブロック線図

今回は、上図のようなブロック線図を取り扱っています。

ブロック線図を簡略化を行う方法には

内部信号を用いる
ブロック線図の特性を利用する

と大きく２つの方法がありますが、本記事では前回からの続きとして１つ目の内部信号を用いる方法を紹介しています。

前回の記事はこちらから

２つ目のブロック線図の特性を利用する方法については、こちらの記事を参考にしてください。

ブロック線図を簡略化する：ブロック線図の特性を利用する方法複雑なブロック線図を１つにまとめるために、簡略化（簡単化）する方法を紹介します。ブロック線図で表されたロボットな...

連立方程式を解く

前回の記事で求めた内部信号と入出力信号の関係式を連立方程式で表します。

内部信号（$E_1(s)$～$E_5(s)$）と出力信号$C(s)$についての式を連立方程式で表すと

$$ \begin{eqnarray} \left\{ \begin{array}{l} E_1(s) &=& R(s) – E_5(s) \\ E_2(s) &=& G_1 E_1(s) + G_8 C(s) \\ E_3(s) &=& G_3 E_2(s) + G_4 E_2(s) \\ E_4(s) &=& E_3(s) – G_6 C(s) \\ E_5(s) &=& G_2 E_2(s) + G_5 E_4(s) \\ C(s) &=& G_7 E_4(s) \end{array} \right.\end{eqnarray} $$

となります。

この連立方程式を解くことで、出力信号$C(s)$を入力信号$R(s)$と伝達要素（$G_1$～$G_8$）で表す式を求めていきます。

出力信号$C(s)$を内部信号$E_2(s)$で表す

出力信号$C(s)$と内部信号の関係式を求めていきます。

出力信号$C(s)$を表す式

$$ C(s) = G_7 E_4(s) $$

に含まれる内部信号$E_4(s)$について、内部信号$E_4(s)$を表す式

$$ E_4(s) = E_3(s) – G_6 C(s) $$

を代入すると

$$ \begin{eqnarray} C(s) &=& G_7 \left(E_3(s) – G_6 C(s)\right) \\ &=& G_7 E_3(s) – G_6 G_7 C(s) \end{eqnarray} $$

と求めることが出来ます。

さらに、この求めた式に含まれる内部信号$E_3(s)$について、内部信号$E_3(s)$を表す式

$$ E_3(s) = G_3 E_2(s) + G_4 E_2(s) $$

を代入することで、出力信号$C(s)$を

$$ \begin{eqnarray} C(s) &=& G_7 \left(G_3 E_2(s) + G_4 E_2(s)\right) – G_6 G_7 C(s) \\ &=& G_7 \left(G_3 + G_4\right) E_2(s) – G_6 G_7 C(s) \end{eqnarray}$$

と表すことができます。

この様に、出力信号$C(s)$と内部信号$E_2(s)$の関係式を求めることが出来ました。

内部信号$E_2(s)$を求める

次に、内部信号$E_2(s)$を求めていきます。

内部信号$E_2(s)$を表す式

$$ E_2(s) = G_1 E_1(s) + G_8 C(s) $$

について、式に含まれる内部信号$E_１(s)$に

$$ E_1(s) = R(s) – E_5(s) $$

を代入して、整理すると

$$ \begin{eqnarray} E_2(s) &=& G_1 \left(R(s) – E_5(s)\right) + G_8 C(s) \\ &=& G_1 R(s) – G_1 E_5(s) + G_8 C(s) \end{eqnarray} $$

のように関係式を求めることが出来ます。

さらに、この関係式に含まれる内部信号$E_5(s)$について、内部信号$E_5(s)$を表す式

$$ E_5(s) = G_2 E_2(s) + G_5 E_4(s) $$

を代入すると

$$ \begin{eqnarray} E_2(s) &=& G_1 R(s) – G_1 \left(G_2 E_2(s) + G_5 E_4(s)\right) + G_8 C(s) \\ &=& G_1 R(s) – G_1 G_2 E_2(s) – G_1 G_5 E_4(s) + G_8 C(s) \end{eqnarray} $$

と求めることが出来ます。

この式を整理して内部信号$E_2(s)$についてまとめると

$$ \begin{eqnarray} E_2(s) + G_1 G_2 E_2(s) &=& G_1 R(s) – G_1 G_5 E_4(s) + G_8 C(s) \\ \left( 1 + G_1 G_2 \right) E_2(s) &=& G_1 R(s) – G_1 G_5 E_4(s) + G_8 C(s) \\ \Rightarrow E_2(s) &=& \frac{G_1 R(s) – G_1 G_5 E_4(s) + G_8 C(s)}{1 + G_1 G_2} \end{eqnarray}$$

となりました。

入力信号$R(s)$と出力信号$C(s)$のみの式を求める

これまでに求めてきた２つの関係式

$$ C(s) = G_7 \left(G_3 + G_4\right) E_2(s) – G_6 G_7 C(s) $$

$$ E_2(s) = \frac{G_1 R(s) – G_1 G_5 E_4(s) + G_8 C(s)}{1 + G_1 G_2} $$

を用いて入力信号$R(s)$と出力信号$C(s)$のみ式を求めていきたいと思います。

１つ目の出力信号$C(s)$の式に含まれる内部信号$E_2(s)$に、２つ目の内部信号$E_2(s)$の式を代入すると

$$ C(s) = G_7 \left(G_3 + G_4\right) \left(\frac{G_1 R(s) – G_1 G_5 E_4(s) + G_8 C(s)}{1 + G_1 G_2}\right) – G_6 G_7 C(s) $$

となります。

この関係式の両辺に$1 + G_1 G_2$を掛けると

$$ \begin{eqnarray} \left(1 + G_1 G_2\right) C(s) &=& \begin{array}{l} G_7 \left(G_3 + G_4\right) \left(G_1 R(s) – G_1 G_5 E_4(s) + G_8 C(s)\right) \\ – G_6 G_7 \left(1 + G_1 G_2\right) C(s) \end{array} \\ &=& \begin{array}{l} G_7 \left(G_3 + G_4\right) G_1 R(s) – G_1 G_5 G_7 \left(G_3 + G_4\right) E_4(s) \\ + G_7 G_8 \left(G_3 + G_4\right) C(s) – G_6 G_7 \left(1 + G_1 G_2\right) C(s) \end{array} \end{eqnarray} $$

と表すことが出来ます。

ここで、求めた関係式に含まれる内部信号$E_4(s)$について、最初の出力信号$C(s)$についての式から

$$ \begin{eqnarray} C(s) &=& G_7 E_4(s) \\ &\Rightarrow& E_4(s) = \frac{C(s)}{G_7} \end{eqnarray} $$

という関係式から導いた値を代入すると

$$ \begin{eqnarray} \left(1 + G_1 G_2\right) C(s) &=& \begin{array}{l} G_1 G_7 \left(G_3 + G_4\right) R(s) – G_1 G_5 G_7 \left(G_3 + G_4\right) \left(\frac{C(s)}{G_7}\right) \\ + G_7 G_8 \left(G_3 + G_4\right) C(s) – G_6 G_7 \left(1 + G_1 G_2\right) C(s) \end{array} \\ &=& \begin{array}{l} G_1 G_7 \left(G_3 + G_4\right) R(s) – G_1 G_5 \left(G_3 + G_4\right) C(s) \\ + G_7 G_8 \left(G_3 + G_4\right) C(s) – G_6 G_7 \left(1 + G_1 G_2\right) C(s) \end{array} \end{eqnarray} $$

となります。

この様に、入力信号$R(s)$と出力信号$C(s)$のみの関係式を求めることが出来ました。

伝達要素$T(s)$を求める

先に求めた入力信号$R(s)$と出力信号$C(s)$の関係式を基に、伝達要素$T(s)$を求めていきたいと思います。

入力信号$R(s)$と出力信号$C(s)$の関係式について、入力信号$R(s)$についての項と出力信号$C(s)$についての項にまとめると

$$ \begin{array}{l} \left(1 + G_1 G_2\right) C(s) + G_1 G_5 \left(G_3 + G_4\right) C(s) \\ – G_7 G_8 \left(G_3 + G_4\right) C(s) + G_6 G_7 \left(1 + G_1 G_2\right) C(s) \end{array} = G_1 G_7 \left(G_3 + G_4\right) R(s) $$

と表されます。

さらに、この関係式を整理すると

$$ \begin{eqnarray} \left[ \begin{array}{l} \left(1 + G_1 G_2\right) + G_6 G_7 \left(1 + G_1 G_2\right) \\ + G_1 G_5 \left(G_3 + G_4\right) – G_7 G_8 \left(G_3 + G_4\right) \end{array} \right] C(s) &=& G_1 G_7 \left(G_3 + G_4\right) R(s) \\ \Rightarrow \left[ \begin{array}{l} \left(1 + G_1 G_2 \right) \left(1 + G_6 G_7\right) \\ + \left( G_1 G_5 – G_7 G_8 \right) \left(G_3 + G_4\right) \end{array} \right] C(s) &=& G_1 G_7 \left(G_3 + G_4\right) R(s) \end{eqnarray} $$

とすることが出来ます。

これより、入力信号$R(s)$と出力信号$C(s)$の関係を示す伝達要素$T(s)$は

$$ T(s) = \frac{C(s)}{R(s)} = \frac{G_1 G_7 \left(G_3 + G_4\right)}{\left(1 + G_1 G_2 \right) \left(1 + G_6 G_7 \right) + \left( G_1 G_5 – G_7 G_8 \right) \left(G_3 + G_4\right)} $$

と求めることが出来ました。