ロボットなどのシステムを表すブロック線図について、複雑なブロック線図を1つの伝達要素で構成されたブロック線図に簡単化する方法を紹介します。
前回の記事では、システムの内部に信号を定義して、各信号の関係式から伝達関数を算出する方法を紹介しました。
今回は、ブロック線図の特性を利用して、複雑なブロック線図を簡単化する手法を紹介します。
ブロック線図の特性について詳しく知りたい方は、是非こちらの記事を参考にしてください。
取り扱うブロック線図
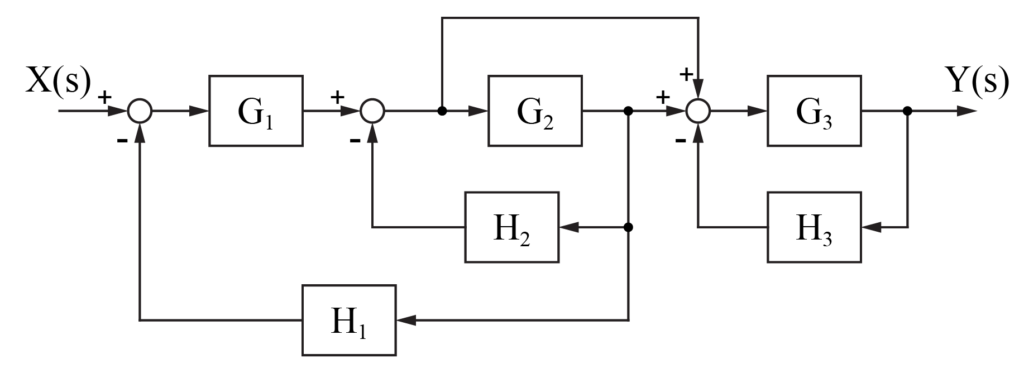
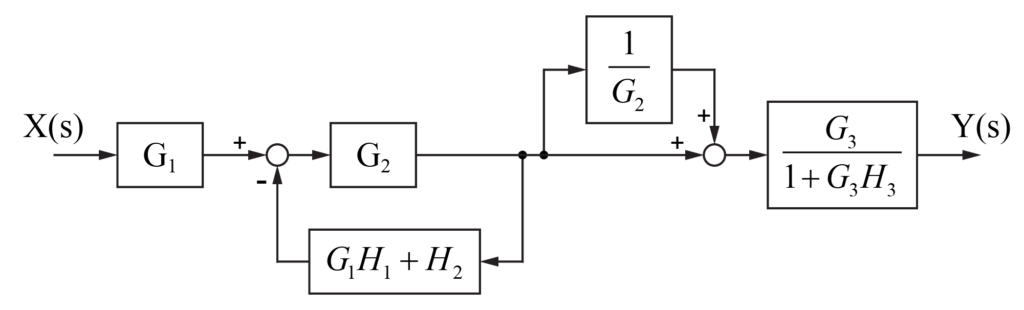
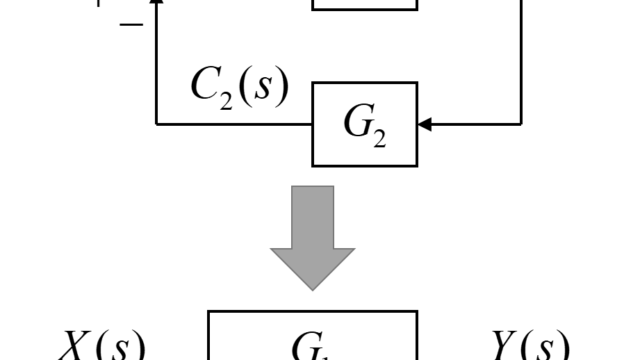
図のように表されるシステムについて、入力X(s)が与えられた時のシステムの出力Y(s)を求めます。
システム内には、伝達要素が6つ、加え合わせ点が3つ、引き出し点が3つ含まれています。
このような複雑なブロック線図を伝達要素が1つだけのブロック線図に変換していきます。
ブロック線図を簡単化することで、複雑なシステムを取り扱いやすくなります。
ブロック線図を簡単化する
与えられたブロック線図について、G3の手前の加え合わせ点に注目します。
加え合わせ点は自由に加え合わせる順を変更することが出来るので、３つの信号を同時に計算していたものを、2つの信号の足し算をした後に、残りの信号の引き算を行う形にします。
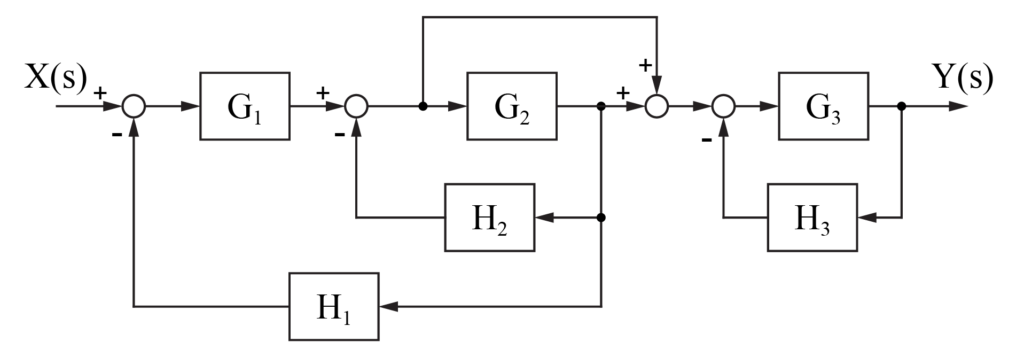
これより、G3とH3の部分が独立したフィードバックの形になるため、1つの伝達関数にまとめます。
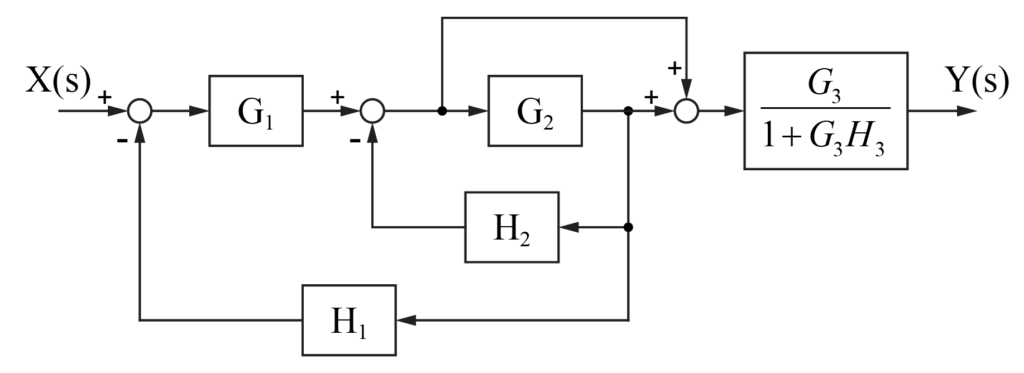
次に、G1とその手前の加え合わせ点に注目します。
加え合わせ点の後ろのG1を加え合わせ点の手前にもっていくため、加え合わせ点に入っている信号の両方G1を追加します。
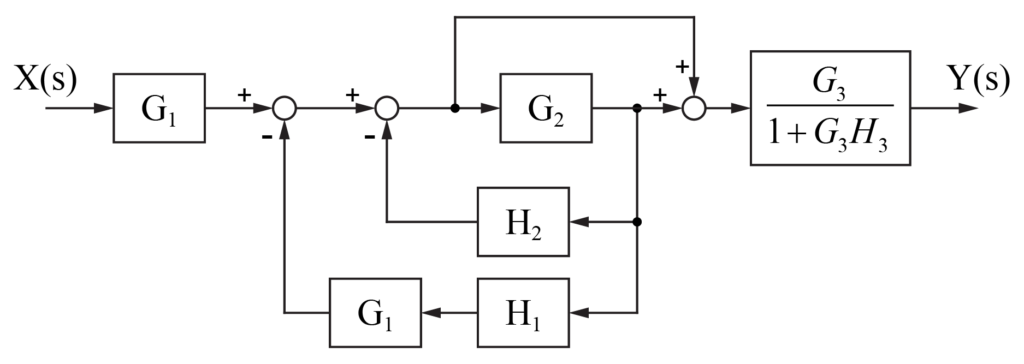
２つの連続した加え合わせ点はまとめることが可能です。
よって、G1とH1からなるフィードバックとH2のフィードバックをまとめることが出来ます。
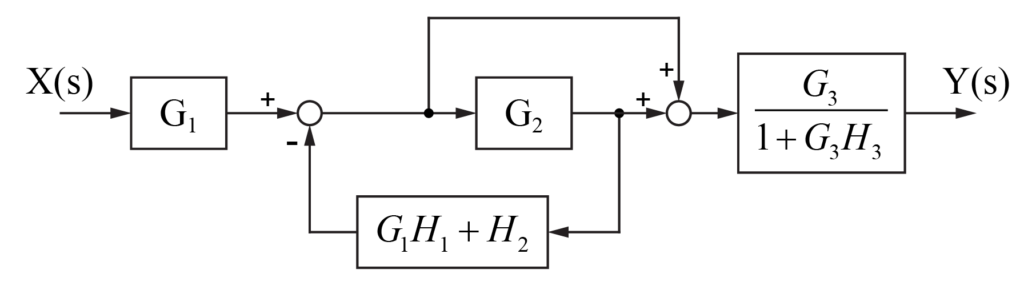
次にG2に注目して、G2を引き出し点の後ろから、前に移動させます。
その際に、G2を迂回していた信号にもG2が掛かってしまうため、1/G2で補償します。
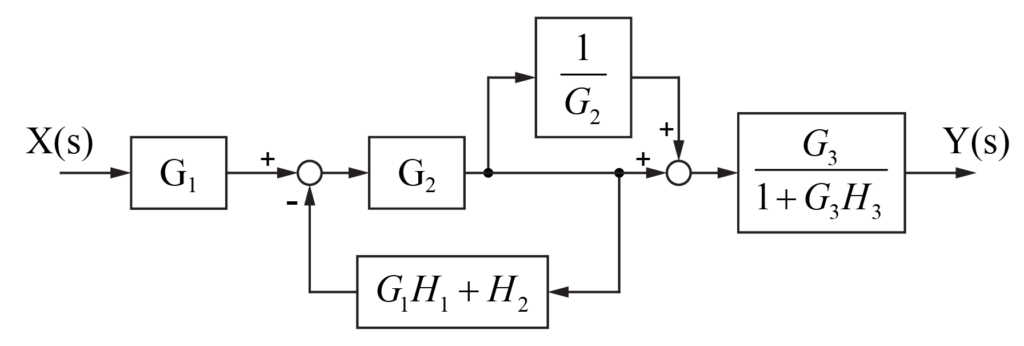
ここで、連続する引き出し点は順序を変更することが出来るため、G2の後ろの2つの引き出し点の順序を入れ替えます。
これより、独立したフィードバック部分とフィードフォワード部分に分けることが出来たので、それぞれの伝達関数を計算します。
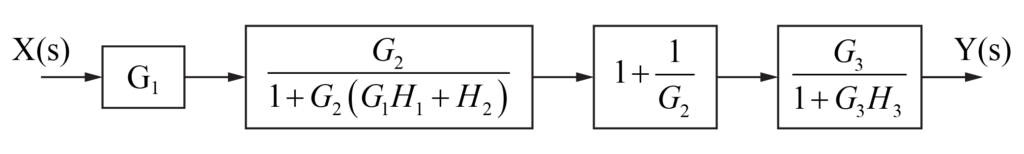
よって、このシステム全体の伝達関数G(s)は、
$$ \begin{eqnarray} G(s) &=& G_1 \frac{G_2}{1+G_2\left(G_1 H_1 + H_2\right)} \left(1 + \frac{1}{G_2}\right) \frac{G_3}{1+G_3 H_3} \\ &=& \frac{G_1 G_3 \left(G_2 + 1\right)}{\left(1+G_2\left(G_1 H_1 + H_2\right) \right) \left(1+G_3 H_3\right) } \end{eqnarray} $$
となることが分かりました。
まとめ
今回は、ブロック線図の特性を利用して、複雑なブロック線図を簡単化する手法を紹介しました。
こちらの記事を併せてご覧いただくと、よりブロック線図の特性を用いた簡単化手法について理解が深まると思います。
当然ですが、今回の方法で求めた伝達関数は、前回の記事にて紹介した内部信号を用いて算出した場合と同じになります。
まだ前回の記事をご覧になってない方は、こちらも併せてご覧ください
合わせて読みたい
ブロック線図の簡略化を簡単に行うコツとして考え方のステップを紹介しています。
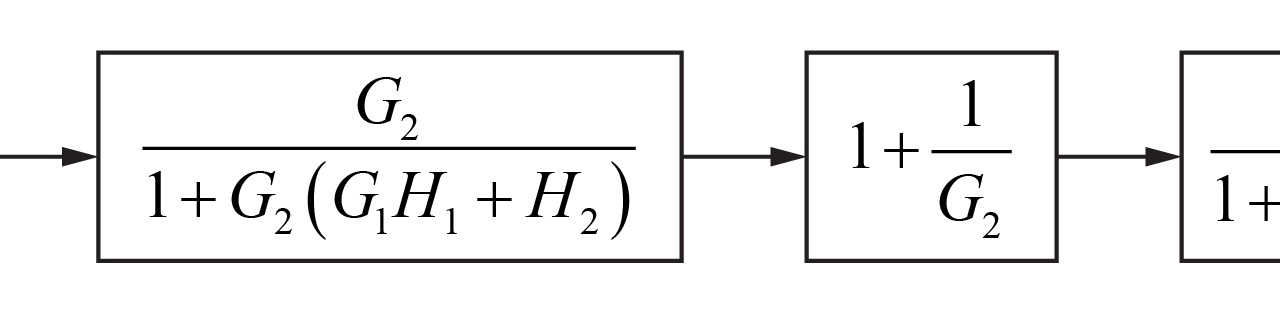
ELEGOO Arduinoスターターキット
UNO R3スマートロボットカー
Raspberry Pi 3 Model b+
