台車の上に倒立振子が設置されているシステムを台車型倒立振子と言います。
この台車型倒立振子を制御するために、システムの状態方程式を求める必要があります。
以前の記事では、台車型倒立振子の運動方程式を求める方法を紹介しました。


今回の記事では、算出した運動方程式から台車型倒立振子モデルの状態方程式を求める方法を紹介します。
台車型倒立振子モデルと運動方程式
今回の記事で取り扱う台車型倒立振子のモデルは下の図のように表されます。
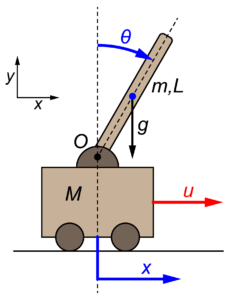
質量Mの台車の上に質量mで長さがLの振り子が上向きに設置されています。
この台車の位置(変位)をx、上向きの振り子(倒立振子)の角度をθとします。
この台車型倒立振子の台車に入力としてuの力を与え、制御するモデルを考えます。
今回の台車型倒立振子モデルについて、運動方程式を求めると
$$ \begin{eqnarray} \left\{ \begin{array}{l} \left( M + m \right) \ddot{x} + \frac{1}{2} m L \cos (\theta) \ddot{\theta} -\frac{1}{2} m L \sin (\theta) \dot{\theta}^2 = u \\ \frac{1}{2} m L \cos (\theta) \ddot{x} – \frac{1}{2} m L \sin (\theta) \dot{x} \dot{\theta} + \frac{1}{3} m L^2 \ddot{\theta} – \frac{1}{2} m g L \sin (\theta) = 0 \end{array} \right. \end{eqnarray} $$
と算出することが出来ます。
詳しい算出方法は、こちらの記事を参考にしてください。


今回の記事では、台車型倒立振子の制御を行うために、この与えられた運動方程式から状態方程式を算出する方法を紹介していきます。
状態方程式の算出
今回の2つの運動方程式には、ともに台車の加速度\(\ddot{x}\)と棒振り子の角加速度\(\ddot{\theta}\)が含まれています。
このままだと状態方程式に変換できないため、2つの運動方程式を連立方程式として扱うことで、加速度\(\ddot{x}\)と角加速度\(\ddot{\theta}\)についての式を求めていきます。
台車の加速度\(\ddot{x}\)について解く
台車の加速度\(\ddot{x}\)を表す式を求めるために、運動方程式による連立方程式から\(\ddot{\theta}\)を消していきます。
式は複雑に見えますが、行うことは通常の連立方程式を解く場合と同様です。
まず\(\ddot{\theta}\)を消すために、1つ目の式に\(\frac{1}{3}\)を掛け、2つ目の式に\(\frac{\cos(\theta)}{2 L}\)を掛けます。
$$ \begin{eqnarray} \left\{ \begin{array}{ll} \left( M + m \right) \ddot{x} + \frac{1}{2} m L \cos (\theta) \ddot{\theta} -\frac{1}{2} m L \sin (\theta) \dot{\theta}^2 = u & \times \frac{1}{3} \\ \frac{1}{2} m L \cos (\theta) \ddot{x} – \frac{1}{2} m L \sin (\theta) \dot{x} \dot{\theta} + \frac{1}{3} m L^2 \ddot{\theta} – \frac{1}{2} m g L \sin (\theta) = 0 & \times \frac{\cos(\theta)}{2 L} \end{array} \right. \end{eqnarray} $$
この処理により\(\ddot{\theta}\)の係数が同じになるため、1つ目の式から2つ目の式を引くことで\(\ddot{\theta}\)を消すことが出来ます。
$$ \begin{eqnarray} \left( \frac{1}{3} \left( M + m \right) -\frac{1}{4} m \cos^2 (\theta) \right) \ddot{x} + \frac{1}{4} m \sin (\theta) \cos (\theta) \dot{x} \dot{\theta} & \\ -\frac{1}{6} m L \sin (\theta) \dot{\theta}^2 + \frac{1}{4} m g \sin (\theta) \cos (\theta) &= \frac{1}{3} u \end{eqnarray} $$
よって、この式を\(\ddot{x}\)について整理すると
$$ \ddot{x} = \frac{-\frac{1}{4} m \sin (\theta) \cos (\theta) \dot{x} \dot{\theta} +\frac{1}{6} m L \sin (\theta) \dot{\theta}^2 – \frac{1}{4} m g \sin (\theta) \cos (\theta) + \frac{1}{3} u}{\frac{1}{3} \left( M + m \right) -\frac{1}{4} m \cos^2 (\theta)} $$
のように、台車の加速度\(\ddot{x}\)を表す式を求めることが出来ました。
棒振り子の角加速度\(\ddot{\theta}\)について解く
同様に、運動方程式による連立方程式から\(\ddot{x}\)を消して、棒振り子の角加速度\(\ddot{\theta}\)について求めていきます。
まず2つの運動方程式について、1つ目の式に\(\frac{1}{2}\cos(\theta)\)を掛け、2つ目の式に\(\frac{ M + m }{m L}\)を掛けます。
$$ \begin{eqnarray} \left\{ \begin{array}{ll} \left( M + m \right) \ddot{x} + \frac{1}{2} m L \cos (\theta) \ddot{\theta} -\frac{1}{2} m L \sin (\theta) \dot{\theta}^2 = u & \times \frac{1}{2} \cos(\theta) \\ \frac{1}{2} m L \cos (\theta) \ddot{x} – \frac{1}{2} m L \sin (\theta) \dot{x} \dot{\theta} + \frac{1}{3} m L^2 \ddot{\theta} – \frac{1}{2} m g L \sin (\theta) = 0 & \times \frac{ M + m }{m L} \end{array} \right. \end{eqnarray} $$
そして、1つ目の式から2つ目の式を引き、\(\ddot{x}\)を式から消します。
$$ \begin{eqnarray} \left(\frac{1}{4} m L \cos^2 (\theta) -\frac{1}{3} \left( M + m \right) L \right) \ddot{\theta} – \frac{1}{4} m L \sin (\theta) \cos (\theta) \dot{\theta}^2 & \\ + \frac{1}{2} \left( M + m \right) \sin (\theta) \dot{x} \dot{\theta} + \frac{1}{2} \left( M + m \right) g \sin (\theta) &= \frac{1}{2} \cos (\theta) u \end{eqnarray} $$
最後に、この式を\(\ddot{\theta}\)について整理することで
$$ \ddot{\theta} = \frac{\frac{1}{4} m L \sin (\theta) \cos (\theta) \dot{\theta}^2 – \frac{1}{2} \left( M + m \right) \sin (\theta) \dot{x} \dot{\theta} – \frac{1}{2} \left( M + m \right) g \sin (\theta) + \frac{1}{2} \cos (\theta) u}{\frac{1}{4} m L \cos^2 (\theta) -\frac{1}{3} \left( M + m \right) L} $$
のように、台車上に設置された棒振り子の角加速度\(\ddot{\theta}\)を表す式を求めることが出来ました。
状態方程式を求める
今回の記事では、台車の変位がxで棒振り子の角度がθと定義された台車型倒立振子モデルについて、状態方程式を求めていきます。
まずは状態ベクトルXを
$$ \boldsymbol{ X } = \begin{bmatrix} x_1 \\ x_2 \\ x_3 \\ x_4 \end{bmatrix} = \begin{bmatrix} x \\ \dot{x} \\ \theta \\ \dot{\theta} \end{bmatrix} $$
と定義します。
この状態ベクトルXに含まれる各要素(x1~x4)について、x1は台車の変位、x2は台車の速度、x3は棒振り子の角度、そしてx4は棒振り子の角速度として定義しています。
そして、状態ベクトルXの時間微分
$$ \boldsymbol{ \dot{X} } = \begin{bmatrix} \dot{x}_1 \\ \dot{x}_2 \\ \dot{x}_3 \\ \dot{x}_4 \end{bmatrix} = \begin{bmatrix} \dot{x} \\ \ddot{x} \\ \dot{\theta} \\ \ddot{\theta} \end{bmatrix} $$
をそれぞれ式(f1~f4)を用いて
$$ \boldsymbol{ \dot{X} } = \begin{bmatrix} \dot{x}_1 \\ \dot{x}_2 \\ \dot{x}_3 \\ \dot{x}_4 \end{bmatrix} = \begin{bmatrix} f_1 (\boldsymbol{ X } , u) \\ f_2 (\boldsymbol{ X } , u) \\ f_3 (\boldsymbol{ X } , u) \\ f_4 (\boldsymbol{ X } , u) \end{bmatrix} $$
のように表すことで、状態方程式を求めていきます。
まず、状態\(\dot{x}_1\)は台車の変位x1の時間微分なので、台車の速度x2になります。
同様に、状態\(\dot{x}_3\)は棒振り子の角度x3の時間微分なので、棒振り子の角速度x4になります。
よって、状態\(\dot{x}_1\)と\(\dot{x}_3\)について
$$ \begin{eqnarray} \left\{ \begin{array}{l} \dot{x}_1 = x_2 \\ \dot{x}_3 = x_4 \end{array} \right. \end{eqnarray} $$
という関係式が成り立ちます。
この関係式と先に求めた台車の加速度と棒振り子の角加速度についての式を用いることで、
$$ \begin{eqnarray} \begin{array} \boldsymbol{ \dot{X} } = \begin{bmatrix} f_1 \\ f_2 \\ f_3 \\ f_4 \end{bmatrix} \\ \left\{ \begin{array}{l} f_1 = \dot{x} \\ f_2 = \frac{-\frac{1}{4} m \sin (\theta) \cos (\theta) \dot{x} \dot{\theta} +\frac{1}{6} m L \sin (\theta) \dot{\theta}^2 – \frac{1}{4} m g \sin (\theta) \cos (\theta) + \frac{1}{3} u}{\frac{1}{3} \left( M + m \right) -\frac{1}{4} m \cos^2 (\theta)} \\ f_3 = \dot{\theta} \\ f_4 = \frac{\frac{1}{4} m L \sin (\theta) \cos (\theta) \dot{\theta}^2 – \frac{1}{2} \left( M + m \right) \sin (\theta) \dot{x} \dot{\theta} – \frac{1}{2} \left( M + m \right) g \sin (\theta) + \frac{1}{2} \cos (\theta) u}{\frac{1}{4} m L \cos^2 (\theta) -\frac{1}{3} \left( M + m \right) L} \end{array} \right. \end{array} \end{eqnarray} $$
のように、状態ベクトルXの時間微分を表すことが出来ます。
ここで各要素の式(f1~f4)を見ると、状態ベクトルXの要素による関数になっていることが分かります。
よって、先ほどの状態ベクトルXの時間微分についての式を
$$ \begin{eqnarray} \boldsymbol{ \dot{X} } &=& \begin{bmatrix} \dot{x}_1 \\ \dot{x}_2 \\ \dot{x}_3 \\ \dot{x}_4 \end{bmatrix} = \begin{bmatrix} f_1(\boldsymbol{X} , u) \\ f_2(\boldsymbol{X} , u) \\ f_3(\boldsymbol{X} , u) \\ f_4(\boldsymbol{X} , u) \end{bmatrix} \\ &=& \begin{bmatrix} x_2 \\ \frac{-\frac{1}{4} m \sin(x_3) \cos(x_3) x_2 x_4 +\frac{1}{6} m L \sin(x_3) {x_4}^2 – \frac{1}{4} m g \sin(x_3) \cos(x_3) + \frac{1}{3} u}{\frac{1}{3} \left( M + m \right) -\frac{1}{4} m \cos^2 (x_3)} \\ x_4 \\ \frac{\frac{1}{4} m L \sin(x_3) \cos(x_3) {x_4}^2 – \frac{1}{2} \left( M + m \right) \sin(x_3) x_2 x_4 – \frac{1}{2} \left( M + m \right) g \sin(x_3) + \frac{1}{2} \cos(x_3) u}{\frac{1}{4} m L \cos^2 (x_3) -\frac{1}{3} \left( M + m \right) L} \end{bmatrix} \end{eqnarray} $$
のように変換することで、台車型倒立振子の状態方程式を求めることが出来ました。
ここで、この算出した状態方程式には、sin関数やcos関数などの非線形関数が含まれています。
そのため、制御を容易にするために状態方程式を線形化する必要があります。
まとめ
今回の記事では、台車型倒立振子の制御を行うために必要となる、状態方程式を算出する方法を紹介しました。
以前の記事で紹介した運動方程式を整理することで、定義した状態ベクトルに対する状態方程式を求めることが出来ました。
次回の記事では、今回算出した状態方程式を線形化する方法を紹介したいと思います。



























 ELEGOO Arduinoスターターキット
ELEGOO Arduinoスターターキット

 UNO R3スマートロボットカー
UNO R3スマートロボットカー

 Raspberry Pi 3 Model b+
Raspberry Pi 3 Model b+
