離散点で不連続な指令値が与えられた場合、ロボット等を連続的で滑らかに制御するために各指令点を補間する必要があります。
3次スプライン補間は、離散的な指令値から連続的で滑らかな軌跡の生成を比較的簡単に実現することが出来ます。
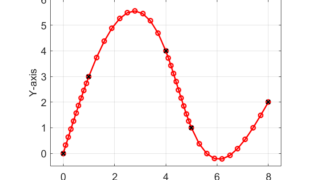
以前の記事では、X-Y平面上の離散的な点を3次スプライン補間を用いて、スムーズな軌跡を作成する方法を紹介しました。
今回は、以前紹介してきた手法の課題とその改善案として、媒介変数を用いた軌跡生成について紹介します。
3次スプライン補間と問題点
離散点\(x_i\)と\(x_{i+1}\)の間を補間する3次多項式\(S_i(x)=y(x)\)を
$$ y(x) = S_i(x) = a_i + b_i (x-x_i) + c_i (x-x_i)^2 + d_i (x-x_i)^3 $$
で表すことで、X-Y平面上の離散点を連続的に補間することが出来ます。
しかし、指令が3次元空間（X軸、Y軸、Z軸）で与えられた場合、この補間式を直接用いることが出来ません。
また、3次多項式\(S_i(x)=y(x)\)では、X軸を変数としてY軸の値を求めていますが、X軸が変化せずY軸のみが変化する場合には、この多項式の関係が成り立たなく場合があります。
この様な場合にも対応するために、媒介変数\(u\)を用いて各軸ごとに離散値を3次スプライン補間する方法を紹介します。
媒介変数を用いた3次スプライン補間
離散点\([x_i,y_i]\)と\([x_{i+1},y_{i+1}]\)の間を補間する3次多項式\(S_i(x)=y(x)\)を
$$ y(x) = S_i(x) = a_i + b_i (x-x_i) + c_i (x-x_i)^2 + d_i (x-x_i)^3 $$
で表す代わりに、媒介変数\(u\)を用いて表していきます。
媒介変数を用いた3次多項式
各軸（X軸とY軸）について、各軸の離散点を補間するためにそれぞれ3次多項式（\(x_i(u)\)と\(y_i(u)\)）を用いて
$$ \begin{eqnarray} x_i(u) &=& f_{x,i}(u) = a_{x,i} + b_{x,i} u + c_{x,i} u^2 + d_{x,i} u^3 \\ y_i(u) &=& f_{y,i}(u) = a_{y,i} + b_{y,i} u + c_{y,i} u^2 + d_{y,i} u^3 \end{eqnarray} $$
と表すことで、X-Y平面上の離散点の補間を行います。
ここで、媒介変数\(u\)は
$$ u = [0, 1] $$
の範囲で定義します。
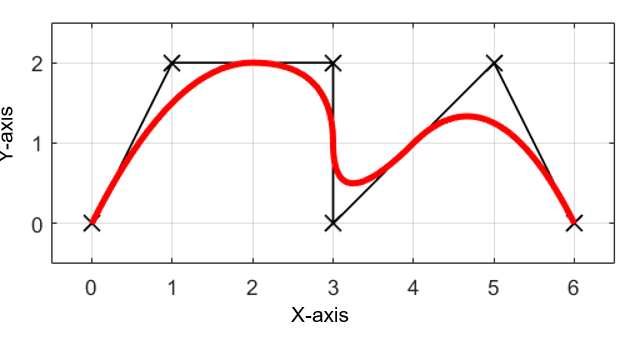
このように、媒介変数\(u\)を用いることで、X軸に変化がなくY軸のみ変化する区間でもスムーズに補間することが出来ます。
指令点が3次元空間の場合
媒介変数\(u\)を用いているため、各軸について独立して扱うことが可能になります。
そのため、X軸とY軸の式に加えてZ軸についての式も考慮することで、離散点\([x_i,y_i,z_i]\)と\([x_{i+1},y_{i+1},z_{i+1}]\)の間を補間する3次多項式を
$$ \begin{eqnarray} x_i(u) &=& f_{x,i}(u) = a_{x,i} + b_{x,i} u + c_{x,i} u^2 + d_{x,i} u^3 \\ y_i(u) &=& f_{y,i}(u) = a_{y,i} + b_{y,i} u + c_{y,i} u^2 + d_{y,i} u^3 \\ z_i(u) &=& f_{z,i}(u) = a_{z,i} + b_{z,i} u + c_{z,i} u^2 + d_{z,i} u^3 \end{eqnarray} $$
のように作成することが出来ます。
3次スプライン補間の各パラメータについては、以前に紹介した方法を同様に求めることが出来ます。
まとめ
本記事では、媒介変数を用いて離散点を3次スプライン補間する方法を紹介しました。
媒介変数を用いることで、与えられた指令の離散点について移動しない軸がある場合や3次元空間で与えられた場合の補間にもそれぞれの軸について3次多項式を求めることで、3次スプライン補間を行うことが出来ます。
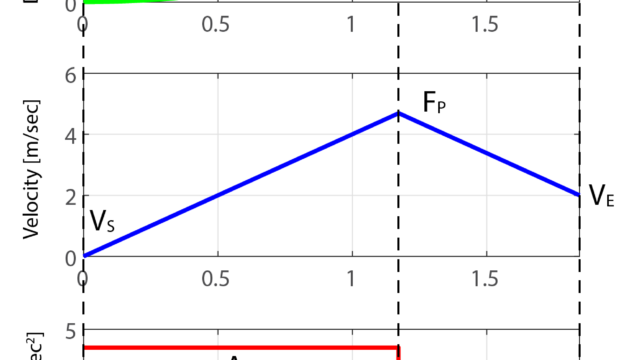
また、媒介変数を用いることで各軸を独立に扱うことが出来るため、速度や加速度を考慮しなければならない場合にも利点があります。
ELEGOO Arduinoスターターキット
UNO R3スマートロボットカー
Raspberry Pi 3 Model b+
