PID制御のブロック線図と伝達関数を表す方法

今回の記事では、制御の世界で広く用いられているPID制御（PID Controller）について説明し、PID制御を用いたフィードバック制御をブロック線図（Block Diagram）と伝達関数（Transfer Function）で表す方法を紹介していきたいと思います。

Contents

PID制御とは
PID制御の入力信号
PID制御のブロック線図
PID制御の伝達関数
まとめ

PID制御とは

PID制御とは、フィードバック制御の内の一つです。

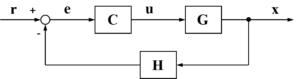
フィードバック制御のブロック線図は下の図のように表されます。

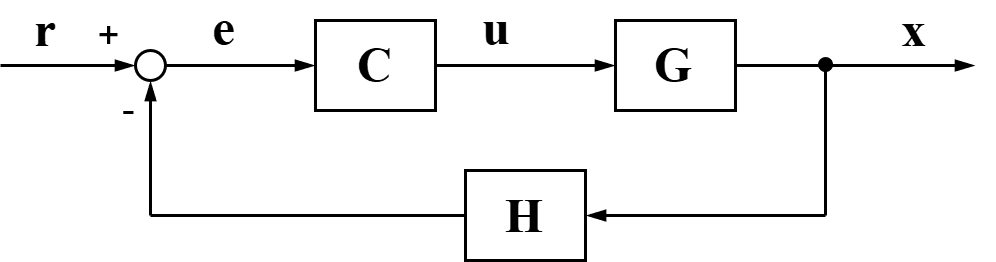
上のフィードバック制御のブロック線図に含まれているコントローラー（C）を

比例要素（Propostional）
積分要素（Integral）
微分要素（Differential）

の3つのパラメータを用いて設計し、偏差eから入力信号uを算出することで、PID制御を行います。

ちなみに、それぞれの英語の頭文字（Propostional、Integral、Differential）をとって、PID制御と呼んでいます。

PID制御の入力信号

以前の記事でも紹介したように、PID制御は比例制御（P制御）、積分制御（I制御）、微分制御（D制御）を組み合わせた制御です。

制御工学の基本　PID制御をマスターしてロボットを動かそう PID制御とはフィードバックを用いた古典制御の中の一つです。その名の通り、現在の出力値$ｙ$について目標値\...

PID制御における時間t領域での入力u(t)は、

$$ u (t) = K_p e (t) + K_i \displaystyle \int_{0}^{t} e (\tau) d\tau + K_d \frac{d e(t)}{dt} $$

という式で表されます。

PID制御のブロック線図や伝達関数を表すために、この時間t領域での入力u(t)をラプラス変換して、周波数s領域の入力U(s)で表す必要があります。

ラプラス変換を用いてシステムを伝達関数で表す前回は、線形時不変システム（LTIシステム）を説明しました。ただ、動的システムに対してLTIシステムのモデルを用いると計...

このPID制御における周波数s領域の入力U(s)は、ラプラス変換を用いて

$$ \begin{eqnarray} U (s) &=& K_p E (s) + \frac{K_i}{s} E (s) + K_d s E (s) \\ &=& \left( K_p + \frac{K_i}{s} + K_d s \right) E (s) \end{eqnarray} $$

という式で表すことが出来ます。

PID制御のブロック線図

先ほど紹介したフィードバック制御のブロック線図に含まれるコントローラーCをPID制御に置き換えて、PID制御のブロック線図を書いていきます。

PID制御のs領域での入力U(s)

$$ U (s) = \left( K_p + \frac{K_i}{s} + K_d s \right) E (s) $$

より、偏差E(s)と入力U(s)の関係を表すように式を変換すると

$$ C (s) = \frac{U (s)}{E (s)} = K_p + \frac{K_i}{s} + K_d s $$

のようにPID制御のコントローラーを表すことが出来ます。

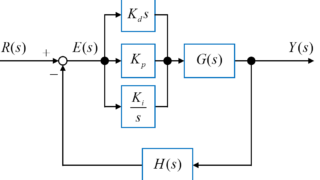
これより、PID制御におけるコントローラーのブロック線図は下図のように表されます。

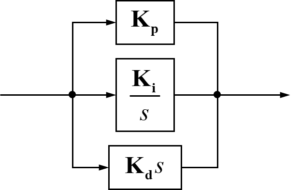
このPID制御部のブロック線図をフィードバック制御のブロック線図に入れると下の図のようになります。

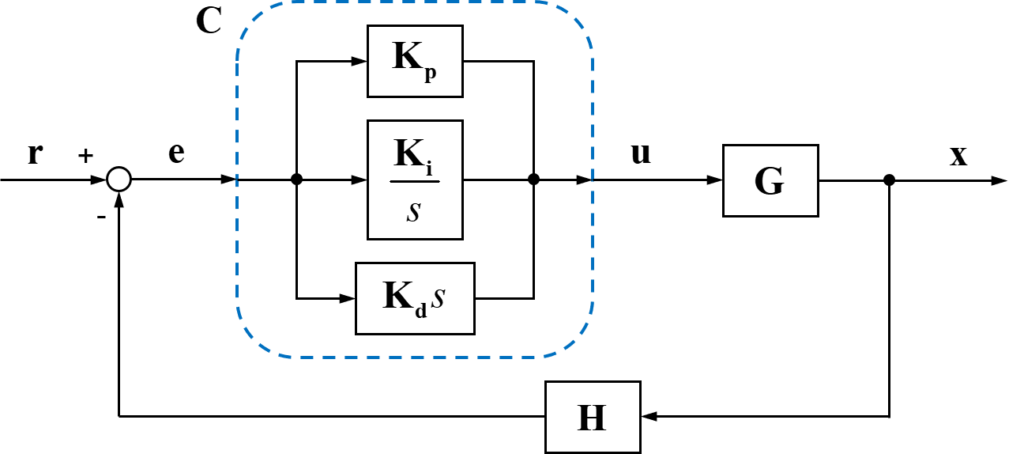
これで、PID制御を用いたフィードバックシステムのブロック線図を書くことが出来ました。

PID制御の伝達関数

今回の記事で取り扱っているPID制御のs領域での入力U(s)は

$$ U (s) = \left( K_p + \frac{K_i}{s} + K_d s \right) E (s) $$

となります。

これより、PID制御部の伝達関数C(s)は

$$ C (s) = \frac{U (s)}{E (s)} = K_p + \frac{K_i}{s} + K_d s $$

と表すことが出来ます。

この式を使ってPID制御を用いたフィードバックシステム全体の伝達関数を求めていきたいと思います。

とは言っても実際に行うことは、フィードバック制御の伝達関数に、PID制御部の伝達関数を代入するだけのシンプルなことです。

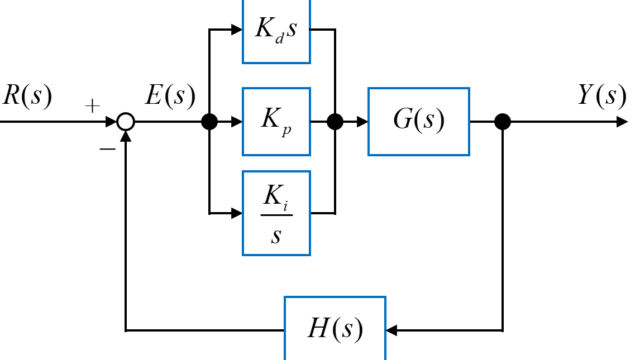
上の図で表されるフィードバック制御の伝達関数T(s)は

$$ T (s) = \frac{X (s)}{R (s)} = \frac{C(s) G(s)}{1 + C(s) G(s) H(s)} $$

となります。

ブロック線図の簡単化ロボットなどのシステムについて、内部の信号の流れを表すためにブロック線図を用いることが多くあります。ロボットなど...

ここで、制御対象G(s)とH(s)を

$$ \begin{eqnarray} \left\{ \begin{array}{l} G(s) = \frac{{K \omega_n}^2}{s^2 + 2 \zeta \omega_n s + {\omega_n}^2} \\ H(s) = 1 \end{array} \right. \end{eqnarray} $$

とすると、PID制御を用いたフィードバック制御の伝達関数は

$$ \begin{eqnarray} T(s) &=& \frac{\left( K_p + \frac{K_i}{s}+ K_d s \right) \frac{K {\omega_n}^2}{s^2 + 2 \zeta \omega_n s + {\omega_n}^2} }{1 + \left( K_p + \frac{K_i}{s}+ K_d s \right) \frac{K {\omega_n}^2}{s^2 + 2 \zeta \omega_n s + {\omega_n}^2} } \\ &=& \frac{\left( K_p + \frac{K_i}{s}+ K_d s \right) {\omega_n}^2}{s^2 + 2 \zeta \omega_n s + {\omega_n}^2 + \left( K_p + \frac{K_i}{s}+ K_d s \right) K {\omega_n}^2} \end{eqnarray} $$

と表すことが出来ます。