運動方程式と伝達関数で２質量の回転運動モデルを表す

回転運動をするシステムについて、実際に２質量の回転運動モデルを用いながら、運動方程式の求め方から伝達関数で表す方法まで紹介していきます。

Contents

回転運動モデル
回転運動モデルの運動方程式
回転運動モデルの伝達関数
- モータ側の伝達関数を求める
- 負荷側の伝達関数を求める
まとめ

回転運動モデル

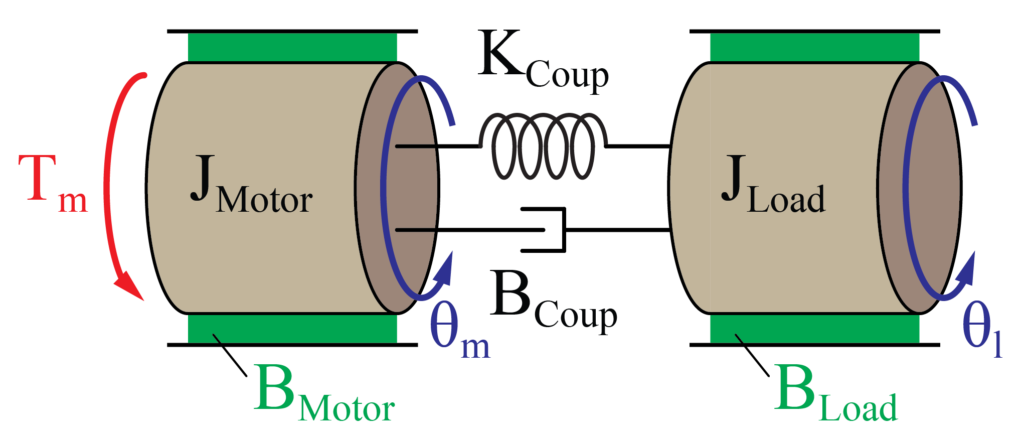
今回は、上の図のような回転運動をする機械システムを取り扱います。

２つの回転体がカップリングで接続された２質量回転運動モデルです。

左側の回転体（モータ側）の慣性モーメントは$J_{Motor}$で、粘性摩擦係数は$B_{Motor}$で表されます。

また、右側の回転体（負荷側）の慣性モーメントは$J_{Load}$で、粘性摩擦係数は$B_{Load}$で表されます。

そして、この２つの回転体（モータと負荷）を接続しているカップリングのばね定数は$K_{Coup}$で、粘性摩擦係数は$B_{Coup}$です。

このシステムにトルク$T_m$をモータ（左側）に与えた場合の各回転体の角変位$\theta_m$と$\theta_l$の様子を求めていきたいと思います。

回転運動モデルの運動方程式

今回の回転運動モデルについて、運動方程式を求めていきます。

基本的な運動方程式の求め方は、回転運動の場合も直線運動の場合も同じです。

直線運動モデルの運動方程式の求め方は、こちらの記事を参考にしてください。

2質量システム（MIMOシステム）の運動方程式を求める MIMO系の状態方程式（状態空間モデル）や伝達関数について、実際に例題を解きながら求めていきたいと思います。 MI...

２質量の直線運動モデルに対する伝達関数の求め方は、こちらの記事を参考にしてください。

伝達関数でMIMOシステム（2質量系）を表すMIMOシステムの例として2質量系モデルを用いて、実際に線形微分方程式（運動方程式）から伝達関数を求める方法を紹介します。...

回転運動モデルと直線運動モデル

回転運動モデルに含まれる

慣性モーメント：$J \ [kg \cdot m^2]$
粘性摩擦係数：$B \ [N \cdot m \cdot s / rad]$
ばね定数：$K \ [N \cdot m / rad]$

は、それぞれ直線運動モデル内の

質量：$M \ [kg]$
ダンパー係数：$C \ [N \cdot s / m]$
ばね定数：$K \ [N / m]$

と同様の特性を持ちます。

この関係を用いて直線運動の場合と同様に、今回の回転運動モデルの運動方程式を求めていきます。

モータ側の運動方程式を求める

まず、モータ側の回転体について運動方程式を求めます。

慣性モーメント$J_{Motor}$による力は、角変位$\theta_m$の２階微分$\ddot{\theta}_m$に比例するため

$$ J_{Motor} \ddot{\theta}_m $$

で表されます。

また、粘性摩擦係数$B_{Motor}$による力は、角変位$\theta_m$の１階微分$\dot{\theta}_m$に比例するため

$$ B_{Motor} \dot{\theta}_m $$

で表されます。

カップリングの粘性摩擦係数$B_{Coup}$による力は、角変位$\theta_m$の１階微分$\dot{\theta}_m$と角変位$\theta_l$の１階微分$\dot{\theta}_l$の差に比例するため

$$ B_{Coup} \left( \dot{\theta}_m – \dot{\theta}_l \right) $$

で求めることが出来ます。

同様に、カップリングのばね定数$K_{Coup}$による力は、角変位$\theta_m$と角変位$\theta_l$の差に比例するため

$$ K_{Coup} \left( \theta_m – \theta_l \right) $$

で求めることが出来ます。

このモータ側の回転体には入力としてトルク$T_m$が与えられています。

算出した力の合計とこの入力のトルク$T_m$は釣り合うため、

$$ J_{Motor} \ddot{\theta}_m + B_{Motor} \dot{\theta}_m + B_{Coup} \left( \dot{\theta}_m – \dot{\theta}_l \right) + K_{Coup} \left( \theta_m – \theta_l \right) = T_m $$

という関係式が導かれます。

よって、このモータ側の回転体についての運動方程式は、

$$ J_{Motor} \ddot{\theta}_m + \left(B_{Motor} + B_{Coup} \right) \dot{\theta}_m + K_{Coup} \theta_m – B_{Coup} \dot{\theta}_l – K_{Coup} \theta_l = T_m $$

で表すことが出来ます。

負荷側の運動方程式を求める

同様に、負荷側の回転体について運動方程式を求めます。

負荷側の回転体に関係する慣性モーメント$J_{Load}$と粘性摩擦係数（B_{Load}とB_{Coup}）、そしてばね定数は$K_{Coup}$による力の合計は

$$ J_{Load} \ddot{\theta}_l + B_{Load} \dot{\theta}_l + B_{Coup} \left( \dot{\theta}_l – \dot{\theta}_m \right) + K_{Coup} \left( \theta_l – \theta_m \right) $$

で求められます。

負荷側には入力としてトルクが与えられていないため、この負荷側の回転体についての運動方程式は、

$$ J_{Load} \ddot{\theta}_l + \left(B_{Load} + B_{Coup} \right) \dot{\theta}_l + K_{Coup} \theta_l – B_{Coup} \dot{\theta}_m – K_{Coup} \theta_m = 0 $$

で表すことが出来ます。

回転運動モデルの伝達関数

算出した２質量の回転運動モデルについての運動方程式

$$ \begin{eqnarray} \left\{ \begin{array}{l} J_{Motor} \ddot{\theta}_m + \left(B_{Motor} + B_{Coup} \right) \dot{\theta}_m + K_{Coup} \theta_m – B_{Coup} \dot{\theta}_l – K_{Coup} \theta_l &=& T_m \\ J_{Load} \ddot{\theta}_l + \left(B_{Load} + B_{Coup} \right) \dot{\theta}_l + K_{Coup} \theta_l – B_{Coup} \dot{\theta}_m – K_{Coup} \theta_m &=& 0 \end{array} \right. \end{eqnarray} $$

から、入力のトルク$T_m$に対する出力の角変位（$\theta_m$と$\theta_l$）の関係を示す伝達関数を基ていきたいと思います。

この運動方程式についてそれぞれラプラス変換を行い時間領域$t$から複素数領域$s$に変換します。

$$ \begin{eqnarray} \left\{ \begin{array}{l} \left( J_{Motor} s^2 + \left(B_{Motor} + B_{Coup} \right) s + K_{Coup} \right) \Theta_m (s) – \left( B_{Coup}s + K_{Coup} \right) \Theta_l (s) &=& T_m (s) \\ \left( J_{Load} s^2 + \left(B_{Load} + B_{Coup} \right) s + K_{Coup} \right) \Theta_l (s) – \left( B_{Coup} s + K_{Coup} \right) \Theta_m (s) &=& 0 \end{array} \right. \end{eqnarray} $$

モータ側の伝達関数を求める

ラプラス変換をした運動方程式から入力$T_m(s)$に対する出力$\Theta_m(s)$を表す伝達関数$G_m (s)$

$$ G_m (s) = \frac{\Theta_m(s)}{T_m(s)} $$

を求めていきます。

運動方程式の２つ目の式

$$ \left( J_{Load} s^2 + \left(B_{Load} + B_{Coup} \right) s + K_{Coup} \right) \Theta_l (s) – \left( B_{Coup} s + K_{Coup} \right) \Theta_m (s) = 0 $$

から、負荷側の角変位$\Theta_l (s) $をモータ側の角変位$\Theta_m (s) $で表すと

$$ \begin{eqnarray} \left( J_{Load} s^2 + \left(B_{Load} + B_{Coup} \right) s + K_{Coup} \right) \Theta_l (s) – \left( B_{Coup} s + K_{Coup} \right) \Theta_m (s) = 0 \\ \Rightarrow \left( J_{Load} s^2 + \left(B_{Load} + B_{Coup} \right) s + K_{Coup} \right) \Theta_l (s) = \left( B_{Coup} s + K_{Coup} \right) \Theta_m (s) \\ \Rightarrow \Theta_l (s) = \frac{B_{Coup} s + K_{Coup}}{J_{Load} s^2 + \left(B_{Load} + B_{Coup} \right) s + K_{Coup}} \Theta_m (s) \end{eqnarray}$$

求めた負荷側の角変位$\Theta_l (s) $についての式を運動方程式の１つ目の式

$$ \left( J_{Motor} s^2 + \left(B_{Motor} + B_{Coup} \right) s + K_{Coup} \right) \Theta_m (s) – \left( B_{Coup}s + K_{Coup} \right) \Theta_l (s) = T_m (s) $$

に代入すると、

$$ \begin{eqnarray} \left( J_{Motor} s^2 + \left(B_{Motor} + B_{Coup} \right) s + K_{Coup} \right) \Theta_m (s) – \left( B_{Coup}s + K_{Coup} \right) \frac{B_{Coup} s + K_{Coup}}{J_{Load} s^2 + \left(B_{Load} + B_{Coup} \right) s + K_{Coup}} \Theta_m (s) &=& T_m (s) \\ \frac{\left( J_{Motor} s^2 + \left(B_{Motor} + B_{Coup} \right) s + K_{Coup} \right)\left( J_{Load} s^2 + \left(B_{Load} + B_{Coup} \right) s + K_{Coup} \right) – \left( B_{Coup}s + K_{Coup} \right)^2}{J_{Load} s^2 + \left(B_{Load} + B_{Coup} \right) s + K_{Coup}} \Theta_m (s) &=& T_m (s) \\ \frac{\left( J_{Motor} s^2 + B_{Motor} s \right) \left( J_{Load} s^2 + B_{Load} s \right) + \left( J_{Motor} s^2 + B_{Motor} s + J_{Load} s^2 + B_{Load} s \right) \left( B_{Coup}s + K_{Coup} \right)}{J_{Load} s^2 + \left(B_{Load} + B_{Coup} \right) s + K_{Coup}} \Theta_m (s) &=& T_m (s) \end{eqnarray} $$

と表すことが出来ます。

これより、求めたいモータ側の伝達関数$G_m (s)$は、

$$ G_m (s) = \frac{J_{Load} s^2 + \left(B_{Load} + B_{Coup} \right) s + K_{Coup}}{\left( J_{Motor} s^2 + B_{Motor} s \right) \left( J_{Load} s^2 + B_{Load} s \right) + \left( J_{Motor} s^2 + B_{Motor} s + J_{Load} s^2 + B_{Load} s \right) \left( B_{Coup}s + K_{Coup} \right)} $$

と算出することが出来ました。

負荷側の伝達関数を求める

同様に、ラプラス変換をした運動方程式から入力$T_m(s)$に対する出力$\Theta_l(s)$を表す伝達関数$G_l (s)$

$$ G_l (s) = \frac{\Theta_l(s)}{T_m(s)} $$

を求めていきたいと思います。

先に求めた負荷側の角変位$\Theta_l (s) $とモータ側の角変位$\Theta_m (s) $の関係式

$$ \Theta_l (s) = \frac{B_{Coup} s + K_{Coup}}{J_{Load} s^2 + \left(B_{Load} + B_{Coup} \right) s + K_{Coup}} \Theta_m (s) $$

に先ほど求めたトルク$T_m(s)$に対するモータ側の角変位$\Theta_m (s) $を表す伝達関数から

$$ \begin{eqnarray} G_m (s) = \frac{\Theta_m(s)}{T_m(s)} = \frac{J_{Load} s^2 + \left(B_{Load} + B_{Coup} \right) s + K_{Coup}}{\left( J_{Motor} s^2 + B_{Motor} s \right) \left( J_{Load} s^2 + B_{Load} s \right) + \left( J_{Motor} s^2 + B_{Motor} s + J_{Load} s^2 + B_{Load} s \right) \left( B_{Coup}s + K_{Coup} \right)} \\ \Rightarrow \Theta_m(s) = \frac{J_{Load} s^2 + \left(B_{Load} + B_{Coup} \right) s + K_{Coup}}{\left( J_{Motor} s^2 + B_{Motor} s \right) \left( J_{Load} s^2 + B_{Load} s \right) + \left( J_{Motor} s^2 + B_{Motor} s + J_{Load} s^2 + B_{Load} s \right) \left( B_{Coup}s + K_{Coup} \right)} T_m(s) \end{eqnarray} $$

と導かれる関係式を代入してトルク$T_m(s)$に対する負荷側の角変位$\Theta_l (s) $の関係式を求めていきます。

負荷側の角変位$\Theta_l (s) $についての式に含まれるモータ側の角変位$\Theta_m (s) $にトルク$T_m(s)$に対するモータ側の角変位$\Theta_m (s) $の関係式を代入すると、

$$ \begin{eqnarray} \Theta_l (s) &=& \frac{B_{Coup} s + K_{Coup}}{J_{Load} s^2 + \left(B_{Load} + B_{Coup} \right) s + K_{Coup}} \frac{J_{Load} s^2 + \left(B_{Load} + B_{Coup} \right) s + K_{Coup}}{\left( J_{Motor} s^2 + B_{Motor} s \right) \left( J_{Load} s^2 + B_{Load} s \right) + \left( J_{Motor} s^2 + B_{Motor} s + J_{Load} s^2 + B_{Load} s \right) \left( B_{Coup}s + K_{Coup} \right)} T_m(s) \\ &=& \frac{B_{Coup} s + K_{Coup}}{\left( J_{Motor} s^2 + B_{Motor} s \right) \left( J_{Load} s^2 + B_{Load} s \right) + \left( J_{Motor} s^2 + B_{Motor} s + J_{Load} s^2 + B_{Load} s \right) \left( B_{Coup}s + K_{Coup} \right)} T_m(s) \end{eqnarray}$$

という負荷側の角変位$\Theta_l (s) $とトルク$T_m(s)$の関係式を導くことが出来ます。

よって、求める負荷側の伝達関数$G_l (s)$は、

$$ G_l (s) = \frac{B_{Coup} s + K_{Coup}}{\left( J_{Motor} s^2 + B_{Motor} s \right) \left( J_{Load} s^2 + B_{Load} s \right) + \left( J_{Motor} s^2 + B_{Motor} s + J_{Load} s^2 + B_{Load} s \right) \left( B_{Coup}s + K_{Coup} \right)} $$

と算出することが出来ました。