今回は、伝達関数モデルから状態空間モデルを求める方法を紹介します。
また、求めた前回求めた状態空間モデルから伝達関数モデルを算出する方法も紹介します。
伝達関数モデルについては、この記事を参考にして下さい。

状態空間モデルは、この記事を参考にして下さい。
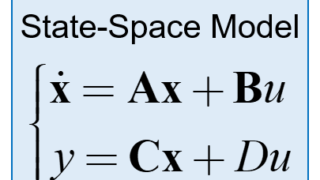
伝達関数から状態空間モデルを算出
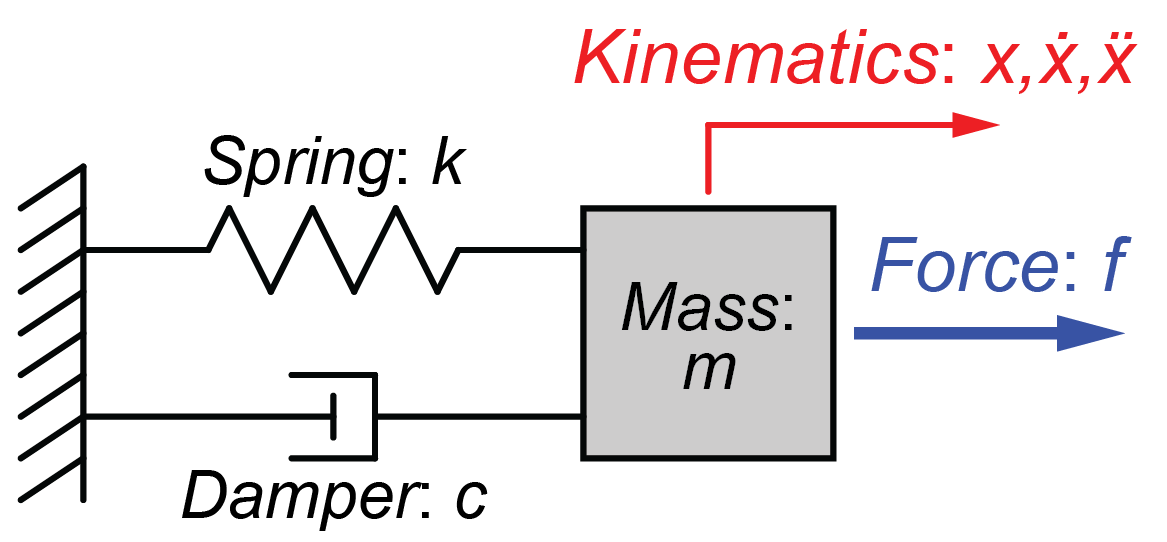
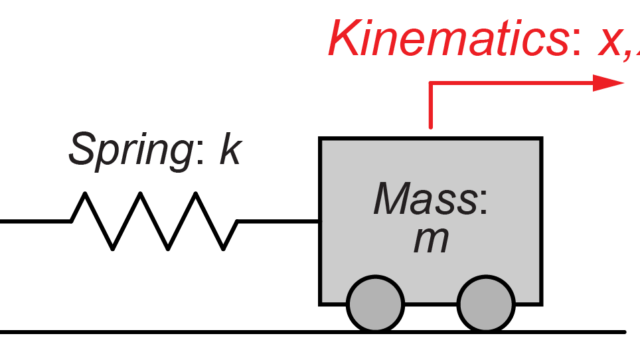
今回は、動的システムとして質量‐ばね‐ダンパーモデルを例に計算していきます。
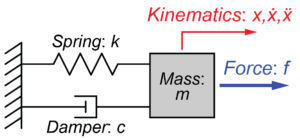
このシステムの伝達関数は入力を\(U(s)\)出力を\(Y(s)\)とすると、
$$ G(s) = \frac{Y(s)}{U(s)} = \frac{N_p(s)}{D_p(s)} = \frac{\frac{1}{m}}{s^2 + \frac{c}{m} s +\frac{k}{m}} $$
と表されます。
この分子\(Y(s) = N_p(s)\)と分母\(U(s) = D_p(s)\)の両方に\(W(s)\)を掛けると、
$$ U(s) = D_p(s) W(s) = s^2 W(s) + \frac{c}{m} s W(s) +\frac{k}{m} W(s) $$
$$ Y(s) = N_p(s) W(s) = \frac{1}{m} W(s) $$
となります。
ここで、状態変数\(X(s)\)を
$$ X_i (s) = s^{i-1} W(s) \quad (i = 1,\ldots,n)$$
とします。
この分子と分母の式について、行列とベクトルを用いた式で表すと、
$$ s \boldsymbol{ X }(s) = \begin{bmatrix} 0 & 1 \\ – \frac{k}{m} & – \frac{c}{m} \end{bmatrix} \boldsymbol{ X }(s) + \begin{bmatrix} 0 \\ 1 \end{bmatrix} U(s) $$
$$ Y(s) = \begin{bmatrix} \frac{1}{m} & 0 \end{bmatrix} \boldsymbol{ X } (s)$$
となります。
この式を逆ラプラス変換すると状態方程式と出力方程式になります。
状態空間モデルから伝達関数への変換
質量‐ばね‐ダンパーシステムの状態空間モデルにおける行列およびベクトルは、
$$ \boldsymbol{ A } = \begin{bmatrix} -\frac{c}{m} & -\frac{k}{m} \\ 1 & 0 \end{bmatrix} , \boldsymbol{ B } = \begin{bmatrix} \frac{1}{m} \\ 0 \end{bmatrix} , \boldsymbol{ C } = \begin{bmatrix} 0 & 1 \end{bmatrix} , D = \begin{bmatrix} 0 \end{bmatrix} $$
となります。
状態空間モデルから伝達関数への変換は、
$$ G(s) = \frac{Y(s)}{U(s)} = \boldsymbol{ C } (s \boldsymbol{ I } – \boldsymbol{ A })^{-1} \boldsymbol{ B } + D $$
で表すことが出来ます。
まとめ
今回は、質量‐ばね‐ダンパーシステムについて、伝達関数モデルと状態空間モデルで表した結果とその関係を紹介しました。
これらのモデルや関係を扱うことで、対象となるシステムを時間空間\(t\)でも複素数空間\(s\)でも取り扱うことが出来ます。

























 ELEGOO Arduinoスターターキット
ELEGOO Arduinoスターターキット

 UNO R3スマートロボットカー
UNO R3スマートロボットカー

 Raspberry Pi 3 Model b+
Raspberry Pi 3 Model b+
